Instructions
Objective
Write a program to add lambda add lambda expressions in haskel..
Requirements and Specifications

Screenshots of output
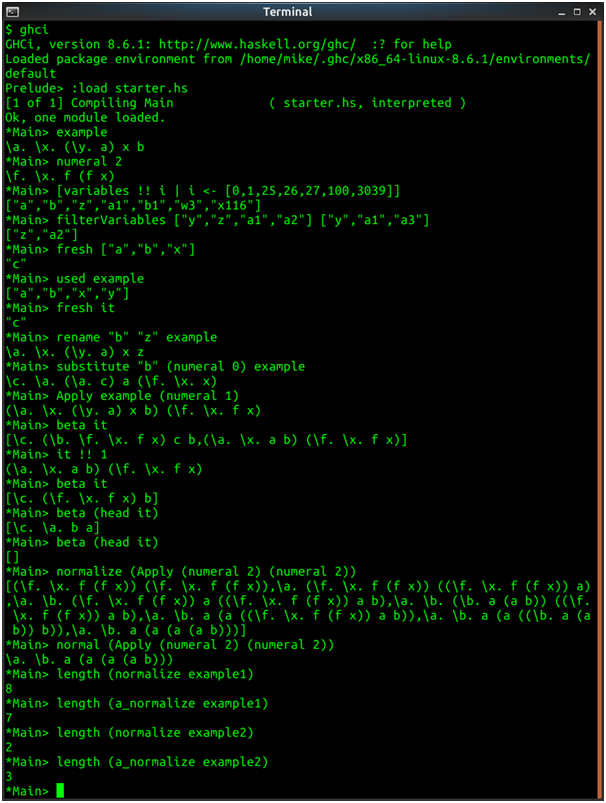
Source Code
type Var = String
data Term =
Variable Var
| Lambda Var Term
| Apply Term Term
-- deriving Show
instance Show Term where
show = pretty
example :: Term
example = Lambda "a" (Lambda "x" (Apply (Apply (Lambda "y" (Variable "a")) (Variable "x")) (Variable "b")))
pretty :: Term -> String
pretty = f 0
where
f i (Variable x) = x
f i (Lambda x m) = if i /= 0 then "(" ++ s ++ ")" else s where s = "\\" ++ x ++ ". " ++ f 0 m
f i (Apply n m) = if i == 2 then "(" ++ s ++ ")" else s where s = f 1 n ++ " " ++ f 2 m
------------------------- Assignment 1
numeral :: Int -> Term
numeral i = Lambda "f" (Lambda "x" (ni i "x" "f"))
where
ni 0 x _ = Variable x
ni n x f = Apply (Variable f) (ni (n - 1) x f)
-------------------------
merge :: Ord a => [a] -> [a] -> [a]
merge xs [] = xs
merge [] ys = ys
merge (x:xs) (y:ys)
| x == y = x : merge xs ys
| x <= y = x : merge xs (y:ys)
| otherwise = y : merge (x:xs) ys
------------------------- Assignment 2
variables :: [Var]
variables = [[c] | c <- ['a'..'z']] ++ [[c]++(show i) |i <- [1..], c <- ['a'..'z']]
filterVariables :: [Var] -> [Var] -> [Var]
filterVariables xs ys = filter (\x -> not (elem x ys)) xs
fresh :: [Var] -> Var
fresh xs = head (filterVariables variables xs)
used :: Term -> [Var]
used (Variable v) = [v]
used (Lambda v t) = merge [v] (used t)
used (Apply x y) = merge (used x) (used y)
------------------------- Assignment 3
rename :: Var -> Var -> Term -> Term
rename x y (Variable z) = Variable (if z == x then y else z)
rename x y l@(Lambda z n) = if z == x then l else Lambda z (rename x y n)
rename x y (Apply n m) = Apply (rename x y n) (rename x y m)
substitute :: Var -> Term -> Term -> Term
substitute x n (Variable y) = if y == x then n else Variable y
substitute x n l@(Lambda y m) = if y == x then l else Lambda z (substitute x n ((rename y z) m))
where
z = fresh ((used m) ++ (used n) ++ [x])
substitute x n (Apply m1 m2) = Apply (substitute x n m1) (substitute x n m2)------------------------- Assignment 4
beta :: Term -> [Term]
beta (Apply l@(Lambda x n) m) = [substitute x m n] ++ (map (\x -> (Apply x m)) (beta l)) ++ (map (\y -> (Apply l y)) (beta m))
beta (Variable _) = []
beta (Lambda x n1) = map (\y-> Lambda x y) (beta n1)
beta (Apply n m) = (map (\x -> (Apply x m)) (beta n)) ++ (map (\y -> (Apply n y)) (beta m))
normalize :: Term -> [Term]
normalize t = t : (eval_beta t)
where
eval_beta a = case beta a of
[] -> []
(x:xs) -> x : (eval_beta x)
normal :: Term -> Term
normal t = last (normalize t)
-------------------------
a_beta :: Term -> [Term]
a_beta (Apply l@(Lambda x n) m) = (map (\x -> (Apply x m)) (a_beta l)) ++ (map (\y -> (Apply l y)) (a_beta m)) ++ [substitute x m n]
a_beta (Variable _) = []
a_beta (Lambda x n1) = map (\y-> Lambda x y) (a_beta n1)
a_beta (Apply n m) = (map (\x -> (Apply x m)) (a_beta n)) ++ (map (\y -> (Apply n y)) (a_beta m))
a_normalize :: Term -> [Term]
a_normalize t = t : (eval_beta t)
where
eval_beta a = case a_beta a of
[] -> []
(x:xs) -> x : (eval_beta x)
a_normal :: Term -> Term
a_normal t = last (a_normalize t)
-------------------------
example1 :: Term
example1 = Apply (Apply (numeral 2) (numeral 2)) (Variable "s")
example2 :: Term
example2 = Apply (Lambda "p" (Lambda "q" (Variable "q"))) (Apply (Lambda "a" (Variable "b")) (Lambda "c" (Variable "d")))