Parity Bits and Hamming Code
The blog explains how to convert the program to hexadecimal using Parity Bits.
Converting the program to hexadecimal
The machine language program is shown in binary below, including the explanation of each step:
0000 1100 0001 0000 0000 0001 0000 ; Load 2 in A
0003 0110 0001 0000 0000 0001 0010 ; add -3 to A
0006 0110 0001 0000 0000 0001 0100 ; add 6 to A
0009 1110 0001 0000 0000 0001 0110 ; save result
000C 0011 1001 0000 0000 0001 0110 ; output result
000F 0000 0000 ; stop
0010 0000 0000 0000 0010 ; value 2
0012 1111 1111 1111 1101 ; value -3
0014 0000 0000 0000 0110 ; value 6
0016 0000 0000 0000 0000 ; result
Converting to hexadecimal
0000 C1 00 10
0003 61 00 12
0006 61 00 14
0009 E1 00 16
000C 39 00 16
000F 00
0010 00 02
0010 FF FD
0010 00 06
0010 00 00
Finally, by removing the addresses we obtain the format that can be loaded into the Pep/9 simulator:
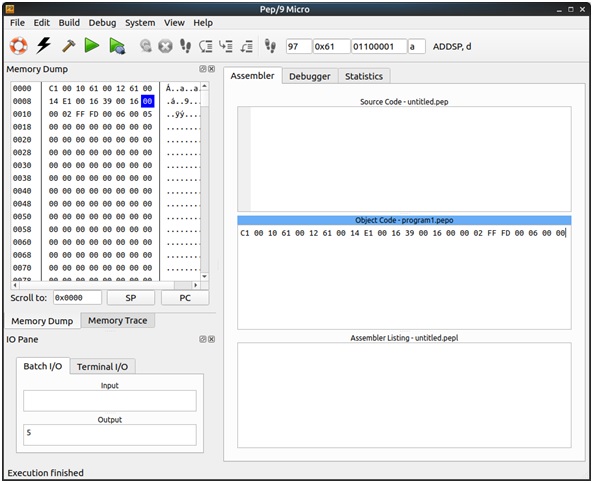
C1 00 10 61 00 12 61 00 14 E1 00 16 39 00 16 00 00 02 FF FD 00 06 00 00
The result of loading and running the program is shown in the screenshot below:
We start from the rightmost hexadecimal digit and we multiply each digit by the corresponding power of 16, starting from zero. Knowing that the letter digits in hexadecimal correspond to a= 10, b= 11,…, f = 15 we obtain:
0xabcdef12 = 2 * 160 + 1 * 161 + f * 162 + e * 163 + d * 164 + c * 165 + b * 166 + a * 167
= 2 * 160 + 1 * 161 + 15 * 162 + 14 * 163 + 13 * 164 + 12 * 165 + 11 * 166 + 10 * 167
= 2 * 1 + 1 * 16 + 15 * 256 + 14 * 4096 + 13 * 65536 + 12 * 1048576 +
11 * 16777216 + 10 * 268435456
= 2 + 16 + 3840 + 57344 + 851968 + 12582912 + 184549376 + 2684354560
= 2882400018
Thus, 0xabcdef12 = 2882400018.
Since the message is 7 bits long we need at least 4 parity bits to cover it, thus the hamming code message will be 11 bits long.
We mark the bit positions, we put the data in the positions that are not powers of 2, the remaining are the parity bits:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| _ | _ | 1 | _ | 0 | 0 | 0 | _ | 1 | 1 | 0 |
Parity in bit 1 corresponds to all odd positions so:
Parity1 = positions 3, 5, 7, 9, 11 = 1 0 0 1 0, since number of ones is even, parity1 is set to zero
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | _ | 1 | _ | 0 | 0 | 0 | _ | 1 | 1 | 0 |
Parity in bit 2 corresponds to all positions that have bit 2 set:
Parity2 = positions 3, 6, 7, 10, 11 = 1 0 0 1 0, since number of ones is even, parity2 is set to zero
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 0 | 1 | _ | 0 | 0 | 0 | _ | 1 | 1 | 0 |
Parity in bit 4 corresponds to all positions that have bit 4 set:
Parity4 = positions 5, 6, 7 = 0 0 0, since number of ones is even, parity4 is set to zero
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | _ | 1 | 1 | 0 |
Lastly, parity in bit 8 corresponds to all positions that have bit 8 set:
Parity8 = positions 9, 10, 11 = 1 1 0, since number of ones is even, parity8 is set to zero
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
Thus the transmitted hamming code is: 00100000110
We write the number in binary as:
0x0C000000 = 0000 1100 0000 0000 0000 0000 0000 0000
Then we organize the binary bits as the fields of the floating-point number, 1-bit sign, 8-bit exponent, 23 bits fraction:
0 00011000 00000000000000000000000
Thus:
Sign = 0 -> + (positive)
Exponent = 00011000 = 0x18 = 24
And:
Fraction = 0
Following the standard, the number is:
Number = sign * 2^(exponent – 127) * ( 1.0 + fraction)
Then:
Number = +2^(24 – 127) * (1.0 + 0)
= +2^-103 * 1.0
Finally:
Number = 9.860761315262648e-32