Instructions
Objective
Write a program in Haskell to create and implement functions for manipulating trees.
Requirements and Specifications
Applying Functions to Trees Background Material
There are many possible variants of the type of binary trees introduced in the Lecture Notes.
Notice how now, the tree stores two different types of data: an element of type `a` at each fork and an element of type
`b` at each leaf.
Implementation Task
Your task is to write a haskell assignment higher-order function `applyfuns` that takes two functions `f :: a -> c` and `g :: b -> d`, as well as an element of type `Tree a b` as input and applies the first function to the values found at the forks, and the second function to the values found at the leaves. That is, implement the function:
```haskell
applyfuns :: (a -> c) -> (b -> d) -> Tree a b -> Tree c d
applyfuns = undefined
```
Screenshots of output
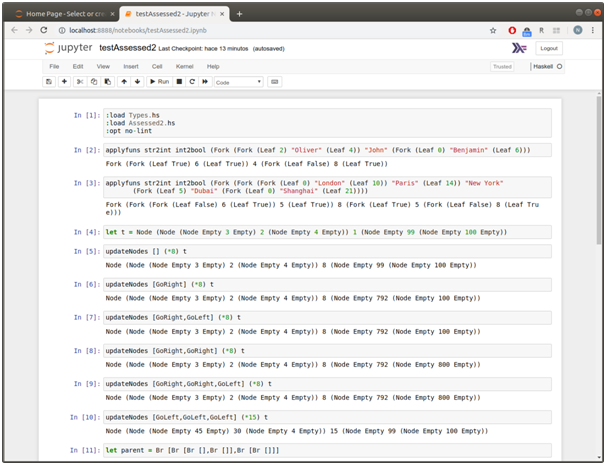
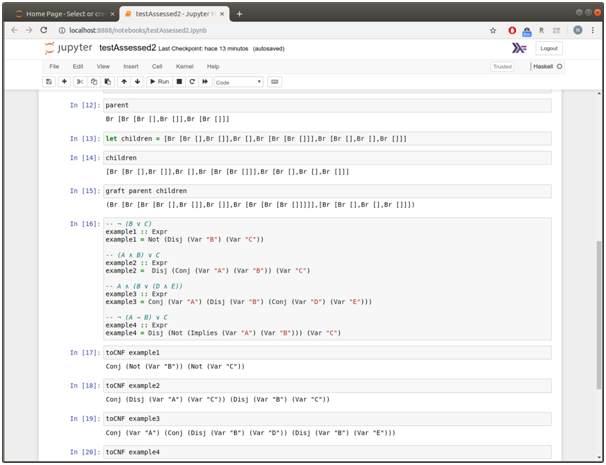
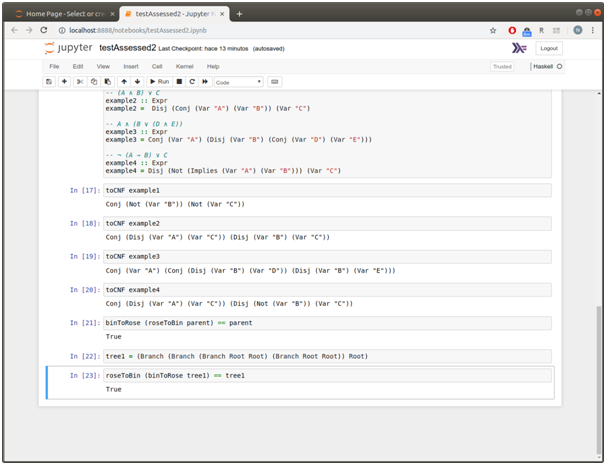
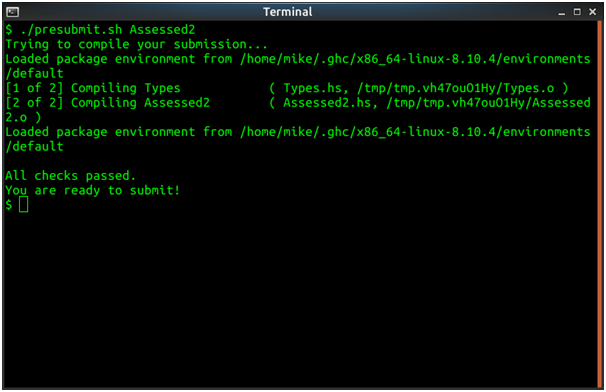
Source Code
-- setting the "warn-incomplete-patterns" flag asks GHC to warn you
-- about possible missing cases in pattern-matching definitions
{-# OPTIONS_GHC -fwarn-incomplete-patterns #-}
-- see https://wiki.haskell.org/Safe_Haskell
{-# LANGUAGE Safe #-}
module Assessed2 (applyfuns , updateNodes , graft , elimImplications ,
isInCNF , toCNF , binToRose , roseToBin) where
import Types
---------------------------------------------------------------------------------
---------------- DO **NOT** MAKE ANY CHANGES ABOVE THIS LINE --------------------
---------------------------------------------------------------------------------
{- Exercise 1 -}
applyfuns :: (a -> c) -> (b -> d) -> Tree a b -> Tree c d
applyfuns _ fleaf (Leaf x) = Leaf (fleaf x) -- if leaf, apply second function
applyfuns ffork fleaf (Fork lt x rt) = -- if fork, apply first function and recurse
Fork (applyfuns ffork fleaf lt) (ffork x) (applyfuns ffork fleaf rt)
{- Exercise 2 -}
updateNodes :: Route -> (a -> a) -> BinTree a -> BinTree a
updateNodes _ _ Empty = Empty -- if leaf, end
updateNodes [] f (Node lt x rt) = Node lt (f x) rt -- if empty route, apply to root and end
-- if left, apply to this node and recurse left
updateNodes (GoLeft:ts) f (Node lt x rt) = Node (updateNodes ts f lt) (f x) rt
-- if right, apply to this node and recurse right
updateNodes (GoRight:ts) f (Node lt x rt) = Node lt (f x) (updateNodes ts f rt)
{- Exercise 3 -}
graft :: Rose -> [ Rose ] -> (Rose , [ Rose ])
-- if leaf, append head of list, return grafted tree and tail
graft (Br []) (br:tl) = (br, tl)
graft (Br brlst) ls =
let (nbrs, nlst) = graftList brlst ls in -- graft nodes in list
(Br nbrs, nlst) -- return new tree with the grafted nodes and the resulting list
where
-- graft a list of nodes
graftList [] gs = ([], gs) -- if we reached the end of list, return empty list and remaining
graftList (hb:tb) gs = -- if the list has more elements
let (rb, lb) = graft hb gs in -- process head, save the result
let (rs, rl) = graftList tb lb in -- recurse to process rest of list, save result
(rb:rs, rl) -- combine head result with tail list result, return it with the remaining list
{- Exercise 4 -}
elimImplications :: Expr -> Expr
elimImplications (Not p) = Not (elimImplications p)
elimImplications (Conj p q) = Conj (elimImplications p) (elimImplications q)
elimImplications (Disj p q) = Disj (elimImplications p) (elimImplications q)
-- replace p-> q by ~p v q
elimImplications (Implies p q) = Disj (Not (elimImplications p)) (elimImplications q)
elimImplications (Var s) = Var s
isInCNF :: Expr -> Bool
isInCNF expr
| isClause expr = True -- is cnf if it's a clause
| otherwise =
case expr of
(Conj p q) -> isInCNF p && isInCNF q -- it's cnf if it's a conjunction of cnf's
_ -> False -- else, it's not a cnf
where
isClause (Var _) = True -- literal is a clause
isClause (Not (Var _)) = True -- negation of literal is a clause
isClause (Disj p q) = isClause p && isClause q -- Clause v Clause is a clause
isClause _ = False -- anything else is not a clause
toCNF :: Expr -> Expr
toCNF e = simpDistrib (simpNegations (simpDeMorgan (simpNegations (elimImplications e))))
where
simpNegations (Not (Not p)) = p
simpNegations (Conj p q) = Conj (simpNegations p) (simpNegations q)
simpNegations (Disj p q) = Disj (simpNegations p) (simpNegations q)
simpNegations x = x -- vars are not simplified
simpDeMorgan (Not (Disj p q)) = Conj (Not (simpDeMorgan p)) (Not (simpDeMorgan q))
simpDeMorgan (Not (Conj p q)) = Disj (Not (simpDeMorgan p)) (Not (simpDeMorgan q))
simpDeMorgan (Not p) = Not (simpDeMorgan p)
simpDeMorgan (Disj p q) = Disj (simpDeMorgan p) (simpDeMorgan q)
simpDeMorgan (Conj p q) = Conj (simpDeMorgan p) (simpDeMorgan q)
simpDeMorgan x = x
simpDistrib (Disj p (Conj q r)) = let simpp = simpDistrib p in
Conj (Disj simpp (simpDistrib q)) (Disj simpp (simpDistrib r))
simpDistrib (Disj (Conj p q) r) = let simpr = simpDistrib r in
Conj (Disj (simpDistrib p) simpr) (Disj (simpDistrib q) simpr)
simpDistrib (Not p) = Not (simpDistrib p)
simpDistrib (Disj p q) = Disj (simpDistrib p) (simpDistrib q)
simpDistrib (Conj p q) = Conj (simpDistrib p) (simpDistrib q)
simpDistrib x = x
{- Exercise 5 -}
binToRose :: Bin -> Rose
binToRose Root = Br [] -- leaf is an empty rose
-- use helper to fill rose tree if root doesn't have left
binToRose (Branch Root r) = Br (binToRosePar r [])
where
-- par is the current parent list of nodes
binToRosePar Root par = par -- if we reached a leaf, return the list of parent nodes
binToRosePar (Branch l r) par =
let narch = binToRosePar r [] in -- convert right child
let parch = binToRosePar l par in -- convert left child
-- add current node using converted right child as its list of nodes,
-- to the parent nodes after left child has been added
(Br narch):parch
-- else, convert directly to binary rose
binToRose (Branch l r) = binToRoseB (Branch l r)
where
binToRoseB Root = Br []
binToRoseB (Branch l r) = Br [binToRoseB l, binToRoseB r]
roseToBin :: Rose -> Bin
roseToBin root
| isBin root = roseToBinB root -- if is a binart, convert directly
| otherwise = roseToBinSib [root] -- process as a node without siblings
where
roseToBinSib [] = Root -- if no more siblings, is a leaf
-- if there is a node, create branch, add siblings to the left and
-- children of this node to the right
roseToBinSib ((Br chs):ss) = Branch (roseToBinSib ss) (roseToBinSib chs)
roseToBinB (Br []) = Root
roseToBinB (Br [l,r]) = Branch (roseToBinB l) (roseToBinB r)
roseToBinB _ = Root
isBin (Br []) = True
isBin (Br [_]) = False
isBin (Br (l:r:[])) = isBin l && isBin r
isBin (Br _) = False