Implementing Keil recursive functions in ARM assembly assignment

Implementing recursive functions using ARM assembly in Keil homework help

The homework deals with implementing the solution to the Hanoi tower problem using ARM assembly. The program uses a recursive function to implement the solution. The function follows the ARM calling convention and saves the used registers on the stack. The number of required moves is calculated by the function and returned to the main program. The program is simulated on the Keil IDE. Here is the solution to demonstrate the quality of work delivered via our ARM assembly homework help service.

Using Recursive Functions to Solve Hanoi Tower Problem in Keil IDE

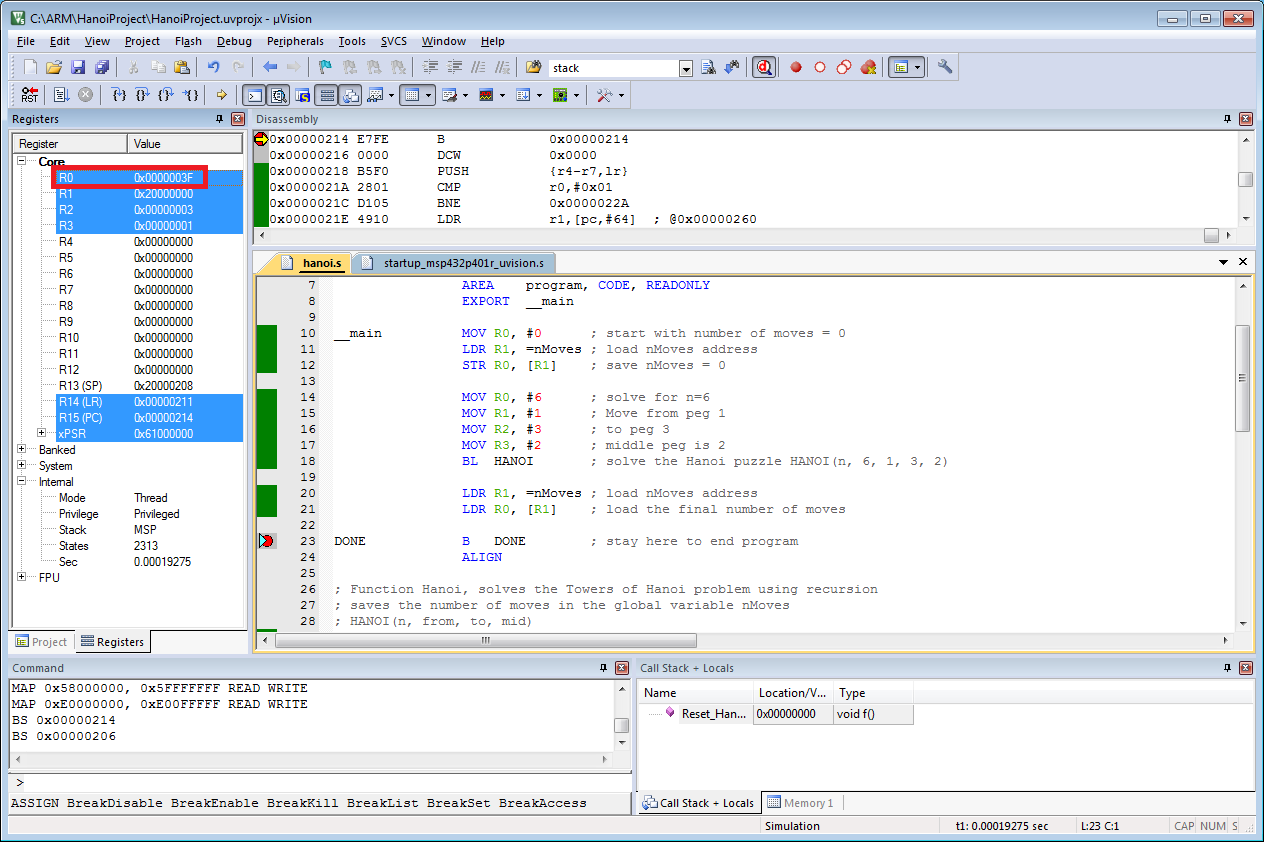
Implementing recursive functions using ARM assembly in Keil assignment help

Solution
; Program to solve the Towers of Hanoi problem for 6 disks
AREA data, ALIGN=2
nMoves SPACE 4
GLOBAL __main
AREA program, CODE, READONLY
EXPORT __main
__main MOV R0, #0 ; start with number of moves = 0
LDR R1, =nMoves ; load nMoves address
STR R0, [R1] ; save nMoves = 0
MOV R0, #6 ; solve for n=6
MOV R1, #1 ; Move from peg 1
MOV R2, #3 ; to peg 3
MOV R3, #2 ; middle peg is 2
BL HANOI ; solve the Hanoi puzzle HANOI(n, 6, 1, 3, 2)
LDR R1, =nMoves ; load nMoves address
LDR R0, [R1] ; load the final number of moves
DONE B DONE ; stay here to end program
ALIGN
; Function Hanoi, solves the Towers of Hanoi problem using recursion
; saves the number of moves in the global variable nMoves
; HANOI(n, from, to, mid)
HANOI PUSH {R4-R7, LR} ; save registers
CMP R0, #1 ; if we are solving for 1 disk
BNE HANOI_MOVE ; if it's not 1, make move
LDR R1, =nMoves ; load nMoves address
LDR R0, [R1] ; load current number of moves
ADD R0, R0, #1 ; increment 1 move
STR R0, [R1] ; update moves in variable
B HANOI_RETURN ; return to caller
HANOI_MOVE MOV R4, R0 ; save arguments in saved registers
MOV R5, R1
MOV R6, R2
MOV R7, R3
SUB R0, R4, #1 ; pass n - 1 for call
MOV R1, R5 ; pass same from value
MOV R2, R7 ; pass old mid as to for call
MOV R3, R6 ; pass old to as mid for call
BL HANOI ; HANOI(n-1, from, mid, to)
LDR R1, =nMoves ; load nMoves address
LDR R0, [R1] ; load current number of moves
ADD R0, R0, #1 ; increment 1 move
STR R0, [R1] ; update moves in variable
SUB R0, R4, #1 ; pass n - 1 for call
MOV R1, R7 ; pass old mid as from value
MOV R2, R6 ; pass old to as to for call
MOV R3, R5 ; pass old from as mid for call
BL HANOI ; HANOI(n-1, mid, to, from)
HANOI_RETURN POP {R4-R7, LR} ; restore registers
BX LR ; return to caller
ALIGN
END