Instructions
Objective
Write a haskell assignment program to Manipulate binary trees.
Requirements and Specifications
Given a binary search tree t, bstInsert x t is a binary search tree formed by
-- replacing a Tip in t with (Bin x Tip Tip) or t, if t already contains x.
--
-- *HW2> bstInsert 3 bst1
-- Bin 2 (Bin 0 Tip Tip) (Bin 4 (Bin 3 Tip Tip) Tip)
-- *HW2> bstInsert 1 bst1
-- Bin 2 (Bin 0 Tip (Bin 1 Tip Tip)) (Bin 4 Tip Tip)
-- *HW2> bstInsert (-1) bst1
-- Bin 2 (Bin 0 (Bin (-1) Tip Tip) Tip) (Bin 4 Tip Tip)
-- *HW2> bstInsert 2 bst1
-- Bin 2 (Bin 0 Tip Tip) (Bin 4 Tip Tip)
--
-- Note: bstInsert should assume that the tree is a valid binary search tree, meaning
-- that the root is greater than all elements in its left subtree and less than all
-- elements in its right subtree. If bstInsert is given a binary search tree, its output
-- must also be a binary search tree. If bstInsert is given a tree that is not a binary
-- search tree, any convenient output is acceptable.
bstInsert :: Ord a => a -> Tree a -> Tree a
bstInsert = undefined
Screenshots of output
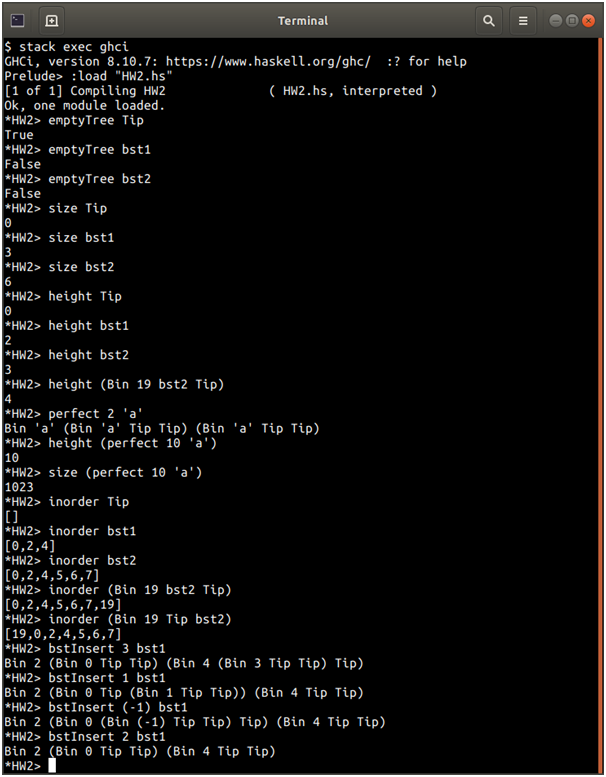
Source Code
module HW2 where
data List a
= Nil
| Cons a (List a)
deriving (Show, Eq, Ord)
data Tree a
= Tip
| Bin a (Tree a) (Tree a)
deriving (Show, Eq, Ord)
bst1 =
Bin 2
(Bin 0 Tip Tip)
(Bin 4 Tip Tip)
bst2 =
Bin 5
bst1
(Bin 7
(Bin 6 Tip Tip)
Tip)
-- 0. emptyTree t returns True if and only if its argument is Tip
emptyTree :: Tree a -> Bool
emptyTree Tip = True
emptyTree _ = False
-- As with HW1, replace each incorrect definition with a correct definition. For example,
--
-- emptyTree Tip = True
-- emptyTree _ = False
-- 1. size t returns the total number of elements in t. This is the same as the number of
-- Bin nodes in t.
--
-- *HW2> size bst1
-- 3
-- *HW2> size bst2
-- 6
size :: Tree a -> Int
size Tip = 0
size (Bin _ lt rt) = size lt + size rt + 1
-- 2. height t returns the height of t. This is the length of the longest path from the
-- root node to a Tip.
--
-- *HW2> height Tip
-- 0
-- *HW2> height bst1
-- 2
-- *HW2> height bst2
-- 3
-- *HW2> height (Bin 19 bst2 Tip)
-- 4height :: Tree a -> Int
height Tip = 0
height (Bin _ lt rt) = max (height lt) (height rt) + 1
-- 3. perfect n a returns a "perfect" binary tree of height n containing the value
-- a for all nodes. In a perfect binary tree, all nodes have either two children
-- or no children.
--
-- *HW2> perfect 2 'a'
-- Bin 'a' (Bin 'a' Tip Tip) (Bin 'a' Tip Tip)
--
-- In general, we expect the following rules to hold:
-- for all positive integers n and all arbitrary values x:
-- height (perfect n x) == n
-- size (perfect n x) == 2^n - 1
perfect :: Int -> a -> Tree a
perfect 0 _ = Tip
perfect 1 x = Bin x Tip Tip
perfect n x = Bin x (perfect (n - 1) x) (perfect (n - 1) x)
-- 4. inorder t returns a list containing all the elements of t in order, meaning the
-- elements of the left subtree (in order), followed by the root, followed by the
-- elements of the right subtree (in order).
--
-- *HW2> inorder Tip
-- []
-- *HW2> inorder bst1
-- [0,2,4]
-- *HW2> inorder bst2
-- [0,2,4,5,6,7]
-- *HW2> inorder (Bin 19 bst2 Tip)
-- [0,2,4,5,6,7,19]
-- *HW2> inorder (Bin 19 Tip bst2)
-- [19,0,2,4,5,6,7]
--
-- In general, for all binary trees t, we expect
-- length (inorder t) == size t
--
-- Note: the order in "inorder" is the order of items in the tree, not their sorted
-- order. Your implementation should not perform any comparisons.
inorder :: Tree a -> [a]
inorder Tip = []
-- if tree, get inorder list from left, append to root element and then append
-- to right inorder list
inorder (Bin x lt rt) = inorder lt ++ [x] ++ inorder rt
-- 5. Given a binary search tree t, bstInsert x t is a binary search tree formed by
-- replacing a Tip in t with (Bin x Tip Tip) or t, if t already contains x.
--
-- *HW2> bstInsert 3 bst1
-- Bin 2 (Bin 0 Tip Tip) (Bin 4 (Bin 3 Tip Tip) Tip)
-- *HW2> bstInsert 1 bst1
-- Bin 2 (Bin 0 Tip (Bin 1 Tip Tip)) (Bin 4 Tip Tip)
-- *HW2> bstInsert (-1) bst1
-- Bin 2 (Bin 0 (Bin (-1) Tip Tip) Tip) (Bin 4 Tip Tip)
-- *HW2> bstInsert 2 bst1
-- Bin 2 (Bin 0 Tip Tip) (Bin 4 Tip Tip)
--
-- Note: bstInsert should assume that the tree is a valid binary search tree, meaning
-- that the root is greater than all elements in its left subtree and less than all
-- elements in its right subtree. If bstInsert is given a binary search tree, its output
-- must also be a binary search tree. If bstInsert is given a tree that is not a binary
-- search tree, any convenient output is acceptable.
bstInsert :: Ord a => a -> Tree a -> Tree a
bstInsert x Tip = Bin x Tip Tip
bstInsert x (Bin y lt rt) =
-- if equal to the value, return the tree
if x == y then (Bin x lt rt)
-- if smaller than value in root, recurse to insert at left subtree
else if x < y then Bin y (bstInsert x lt) rt
-- else, it's greated than value in root, recurse to insert at right subtree
else Bin y lt (bstInsert x rt)