Instructions
Objective
Write an assembly language assignment program to multiply two unsigned 8-bit numbers given in binary as in the following code segment. The value 1100b (in binary) is the multiplicand and 0110b is the multiplier. Both are 8-bit values (the leading zeros are not shown)
Requirements and Specifications
The objective of this assignment is to show how multiplication can be done entirely by using
the shift and add operations. We will consider multiplication of two unsigned 8-bit numbers. In order to use the shift operation, we have to express the multiplier as a power of 2.
For example, if the multiplier is 64, the result can be obtained by shifting the multiplicand
left by six bit positions because 26 = 64.
What if the multiplier is not a power of 2? In this case, we have to express this number as a sum of powers of 2. For example, if the multiplier is 10, it can be expressed as 8 + 2, where each term is a power of 2. Then the required multiplication can be done by two shifts and one addition.
The question now is: How do we express the multiplier in this form? If we look at the binary
representation of the multiplier (10D = 00001010B), there is a 1 in bit positions with weights 8 and 2. Thus, for each 1 bit in the multiplier, the multiplicand should be shifted left by a number of positions equal to the bit position number. In this example, the multiplicand should be shifted left by 3 and 1 bit positions and then added.
Screenshots of output
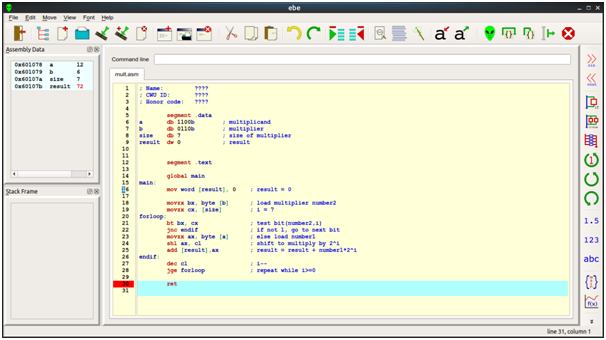
Source Code
; Name: ????
; CWU ID: ????
; Honor code: ????
segment .data
a db 1100b ; multiplicand
b db 0110b ; multiplier
size db 7 ; size of multiplier
result dw 0 ; result
segment .text
global main
main:
mov word [result], 0 ; result = 0
movzx bx, byte [b] ; load multiplier number2
movzx cx, [size] ; i = 7
forloop:
bt bx, cx ; test bit(number2,i)
jnc endif ; if not 1, go to next bit
movzx ax, byte [a] ; else load number1
shl ax, cl ; shift to multiply by 2^i
add [result],ax ; result = result + number1*2^i
endif:
dec cl ; i--
jge forloop ; repeat while i>=0
ret