Instructions
Objective
Write a program to write basic functions in Lisp, check if a list is a palindrome, rotate a list, etc Lisp.
Requirements and Specifications
You may not use any looping constructs, set, setq, etc.
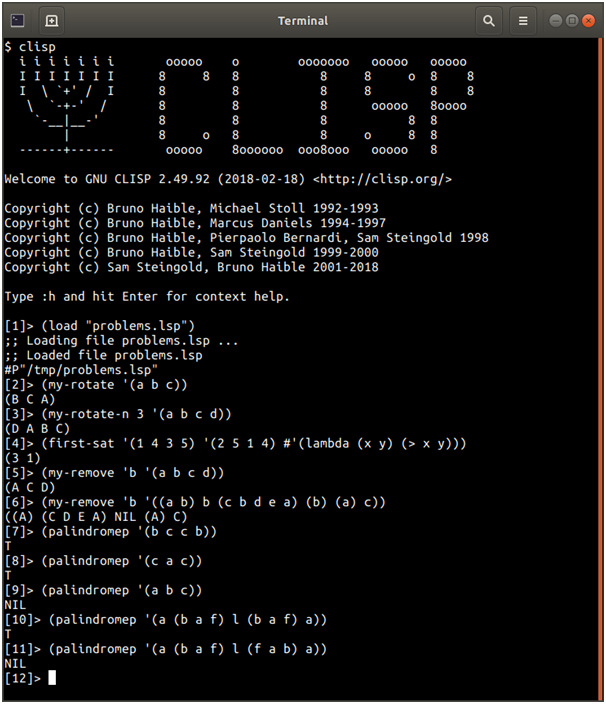
- Write a Lisp assignment called my-rotate that takes a list, pops off the first element and adds it to the end of the list, returning the resulting list. For example: (my-rotate ‘(a b c)) returns (b c a)
- Write a Lisp function called my-rotate-n that takes a number n and a list and performs the “my-rotate” function n times. For example: (my-rotate-n 3 ‘(a b c d)) returns (d a b c).
- Write a Lisp function first-sat that takes two lists and a function foo as arguments. Function foo should take two arguments and return Boolean (t or nil). The result of a call to first-sat should be a list containing the first pair of arguments that satisfies (returns true) from foo. For example: (first-sat ‘(1 4 3 5) ‘(2 5 1 4) #’(lambda (x y) (> x y))) Note that #’ is the same as (function … ) so (first-sat ‘(1 4 3 5) ‘(2 5 1 4) (function (lambda (x y) (> x y)))) returns (3 1).
- Write a Lisp function my-remove that takes an atom and a list as input and returns a list with all instances of the atom removed (including recursive instances). Note that you may not use the Lisp function remove or any related function! Implement this using only one function (no helper functions). For example, (my-remove ‘b ‘(a b c d)) returns (a c d) (my-remove ‘b ‘((a b) b (c b d e a) (b) (a) c)) returns ((a) (c d e a) nil (a) c)
- Write a Lisp function called palindromep that takes a list as input and returns t if the list is a palindrome and nil otherwise. Do NOT use the built-in reverse function or any related function. For example: (palindromep ‘(b c c b)) returns t (palindromep ‘(c a c)) returns t (palindromep ‘(a b c)) returns nil1 (palindromep ‘(a (b a f) l (b a f) a)) returns t (palindromep ‘(a (b a f) l (f a b) a)) returns nil Note that sublists are not examined (this is shown in the last two examples).
Screenshots of output
Source Code
; Problem 1
;----------
(defun my-rotate (lst)
; remove first element and append it at the end of the list
(append (cdr lst) (list (car lst))))
; Problem 2
;----------
(defun my-rotate-n (n lst)
(if (<= n 0)
; if n is 0 leave as it is
lst
; if positive, recurse with n-1 and rotated list
(my-rotate-n (- n 1) (my-rotate lst))))
; Problem 3
;----------
(defun first-sat (lst1 lst2 foo)
(cond
((null lst1) '()) ; if first list is empty, return empty list
((null lst2) '()) ; if first list is empty, return empty list
; if the function of the top elements is true, return a list of the top elements
((funcall foo (car lst1) (car lst2)) (list (car lst1) (car lst2)))
; else, recurse with the remaining elements in both lists
(t (first-sat (cdr lst1) (cdr lst2) foo))))
; Problem 4
;----------
(defun my-remove (x lst)
(cond
; if list is empty, return empty list
((null lst) lst)
; if the first element is a list, remove atom from that list first and
; then append it to the result of removing the atom from the rest of
; the original list
((listp (car lst)) (cons (my-remove x (car lst)) (my-remove x (cdr lst))))
; else it's an atom and if it's equal to the element to be removed,
; recurse with the rest of the list (ignore the first element)
((eq x (car lst)) (my-remove x (cdr lst)))
; if not equal, keep the first element and recurse
(t (cons (car lst) (my-remove x (cdr lst))))))
; Problem 5
;----------
; Helper function to reverse a list
(defun my-reverse (lst)
(if (null lst)
; if empty list, return empty list
'()
; else, append first element at end of reversed list
(append (my-reverse (cdr lst)) (list (car lst)))))
(defun palindromep (lst)
; is a palindrome if the list equals its reverse
(equal lst (my-reverse lst)))