Instructions
Objective
Write a program to write replacement for malloc function in C language.
Requirements and Specifications
Write a scheme assignment recursive function that takes a list of numbers as input and returns a list of the numbers in ascending order.
Use the quicksort algorithm, dividing the lists based upon the midrange value of the list. Use ( 20 13 74 5 12 9 22 95 22 6 101 72 3 53 33 21 96) as input
(myQuicksort ‘( 20 13 74 5 12 9 22 95 22 6 101 72 3 53 33 21 96)).
returns ‘(3 5 6 9 12 13 20 21 22 22 33 53 72 74 95 96 101).
You may not use sort, quicksort, set!, or mean.
It is possible to code this using only functions defined in slides this semester this far.
Your answer is not required to be tail recursive.
Screenshots of output
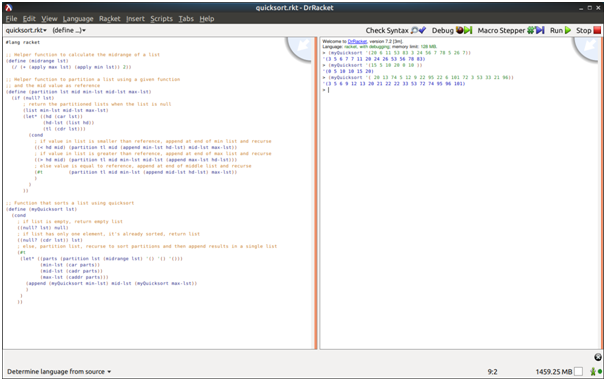
Source Code
#lang racket
;; Helper function to calculate the midrange of a list
(define (midrange lst)
(/ (+ (apply max lst) (apply min lst)) 2))
;; Helper function to partition a list using a given function
;; and the mid value as reference
(define (partition lst mid min-lst mid-lst max-lst)
(if (null? lst)
; return the partitioned lists when the list is null
(list min-lst mid-lst max-lst)
(let* ((hd (car lst))
(hd-lst (list hd))
(tl (cdr lst)))
(cond
; if value in list is smaller than reference, append at end of min list and recurse
((< hd mid) (partition tl mid (append min-lst hd-lst) mid-lst max-lst))
; if value in list is greater than reference, append at end of max list and recurse
((> hd mid) (partition tl mid min-lst mid-lst (append max-lst hd-lst)))
; else value is equal to reference, append at end of middle list and recurse
(#t (partition tl mid min-lst (append mid-lst hd-lst) max-lst))
)
)
))
;; Function that sorts a list using quicksort
(define (myQuicksort lst)
(cond
; if list is empty, return empty list
((null? lst) null)
; if list has only one element, it's already sorted, return list
((null? (cdr lst)) lst)
; else, partition list, recurse to sort partitions and then append results in a single list
(#t
(let* ((parts (partition lst (midrange lst) '() '() '()))
(min-lst (car parts))
(mid-lst (cadr parts))
(max-lst (caddr parts)))
(append (myQuicksort min-lst) mid-lst (myQuicksort max-lst))
)
)
))