Instructions
Objective
Write a racket assignment program that allows users to reduce scheme expressions.
Requirements and Specifications



Screenshots of output
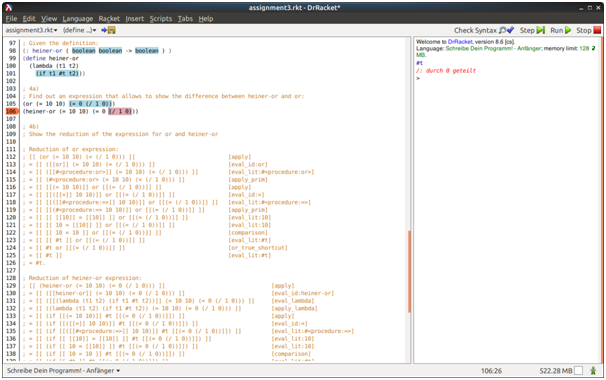
Source Code
;; Die ersten drei Zeilen dieser Datei wurden von DrRacket eingefügt. Sie enthalten Metadaten
;; über die Sprachebene dieser Datei in einer Form, die DrRacket verarbeiten kann.
#reader(lib "beginner-reader.rkt" "deinprogramm" "sdp")((modname assignment3) (read-case-sensitive #f) (teachpacks ()) (deinprogramm-settings #(#f write repeating-decimal #f #t none explicit #f ())))
; 1b)
; Given the definitions
;(define pi 3.1415)
;(define perimeter
; (lambda (r)
; (* 2 pi r)))
; Reduce:
;(perimeter 2)
; Reduction of (perimeter 2):
; [[ (perimeter 2) ]] [apply]
; = [[ ([[perimeter]] 2) ]] [eval_id: perimeter]
; = [[ ([[(lambda (r) (* 2 pi r))]] 2) ]] [eval_lambda]
; = [[ ((lambda (r) (* 2 pi r)) 2) ]] [apply_lambda]
; = [[ (* 2 pi [[2]]) ]] [eval_lit:2]
; = [[ (* 2 pi 2) ]] [apply]
; = [[ ([[*]] 2 pi 2) ]] [eval_id:*]
; = [[ ([[#]] 2 pi 2) ]] [eval_lit:#]
; = [[ (# 2 pi 2) ]] [apply_prim]
; = [[ [[2]] * [[pi]] * [[2]] ]] [eval_lit:2]
; = [[ 2 * [[pi]] * [[2]] ]] [eval_id:pi]
; = [[ 2 * [[3.1415]] * [[2]] ]] [eval_lit:3.1415]
; = [[ 2 * 3.1415 * [[2]] ]] [eval_lit:2]
; = [[ 2 * 3.1415 * 2 ]] [arithmetic]
; = [[ 12.566 ]] [eval_lit:12.566]
; = 12.566.
; 1c)
; Reduce the expression:
;((lambda (a b)
; ((lambda (b)
; (+ b b ))
; a))
; 21 42)
; Reduction of expression:
; [[ ((lambda (a b) ((lambda (b) (+ b b)) a)) 21 42) ]] [apply_lambda]
; = [[ ((lambda (b) (+ b b)) [[21]]) ]] [eval_lit:21]
; = [[ ((lambda (b) (+ b b)) 21) ]] [apply_lambda]
; = [[ (+ [[21]] [[21]]) ]] [eval_lit:21]
; = [[ (+ 21 [[21]]) ]] [eval_lit:21]
; = [[ (+ 21 21) ]] [apply]
; = [[ ([[+]] 21 21) ]] [eval_id:+]
; = [[ ([[#]] 21 21) ]] [eval_lit:#]
; = [[ (# 21 21) ]] [apply_prim]
; = [[ [[21]] + [[21]] ]] [eval_lit:21]
; = [[ 21 + [[21]] ]] [eval_lit:21]
; = [[ 21 + 21 ]] [arithmetic]
; = [[ 42 ]] [eval_lit:42]
; = 42.
; 2a)
;(: less-zero? ( number -> boolean ))
;(define less-zero?
; (lambda (x)
; (if (not (< x 0))
; #f
; #t)))
; Reduced function
(: less-zero? ( number -> boolean ))
(define less-zero?
(lambda (x)
(< x 0)))
; 2b)
;(: f ( number -> boolean ))
;(define f
; ((lambda (x) x)
; (lambda (y)
; (cond
; ((> y 11) #t )
; ((< y 11) #f )
; ((= y 11) #t )))))
; Reduced function
(: f ( number -> boolean ))
(define f
(lambda (x)
(>= x 11)))
; 2c)
;(: gp ( boolean boolean -> boolean ))
;(define gp
; (lambda (a b)
; (or (not b )
; (and a (not a )))))
; Reduced function
(: g ( boolean boolean -> boolean ))
(define g
(lambda (a b)
(not b))); 4)
; Given the definition:
(: heiner-or ( boolean boolean -> boolean ) )
(define heiner-or
(lambda (t1 t2)
(if t1 #t t2)))
; 4a)
; Find out an expression that allows to show the difference between heiner-or and or:
(or (= 10 10) (= 0 (/ 1 0)))
(heiner-or (= 10 10) (= 0 (/ 1 0)))
; 4b)
; Show the reduction of the expression for or and heiner-or
; Reduction of or expression:
; [[ (or (= 10 10) (= (/ 1 0))) ]] [apply]
; = [[ ([[or]] (= 10 10) (= (/ 1 0))) ]] [eval_id:or]
; = [[ ([[#]] (= 10 10) (= (/ 1 0))) ]] [eval_lit:#]
; = [[ (# (= 10 10) (= (/ 1 0))) ]] [apply_prim]
; = [[ [[(= 10 10)]] or [[(= (/ 1 0))]] ]] [apply]
; = [[ [[([[=]] 10 10)]] or [[(= (/ 1 0))]] ]] [eval_id:=]
; = [[ [[([[#]] 10 10)]] or [[(= (/ 1 0))]] ]] [eval_lit:#]
; = [[ [[(# 10 10)]] or [[(= (/ 1 0))]] ]] [apply_prim]
; = [[ [[ [[10]] = [[10]] ]] or [[(= (/ 1 0))]] ]] [eval_lit:10]
; = [[ [[ 10 = [[10]] ]] or [[(= (/ 1 0))]] ]] [eval_lit:10]
; = [[ [[ 10 = 10 ]] or [[(= (/ 1 0))]] ]] [comparison]
; = [[ [[ #t ]] or [[(= (/ 1 0))]] ]] [eval_lit:#t]
; = [[ #t or [[(= (/ 1 0))]] ]] [or_true_shortcut]
; = [[ #t ]] [eval_lit:#t]
; = #t.
; Reduction of heiner-or expression:
; [[ (heiner-or (= 10 10) (= 0 (/ 1 0))) ]] [apply]
; = [[ ([[heiner-or]] (= 10 10) (= 0 (/ 1 0))) ]] [eval_id:heiner-or]
; = [[ ([[(lambda (t1 t2) (if t1 #t t2))]] (= 10 10) (= 0 (/ 1 0))) ]] [eval_lambda]
; = [[ ((lambda (t1 t2) (if t1 #t t2)) (= 10 10) (= 0 (/ 1 0))) ]] [apply_lambda]
; = [[ (if [[(= 10 10)]] #t [[(= 0 (/ 1 0))]]) ]] [apply]
; = [[ (if [[([[=]] 10 10)]] #t [[(= 0 (/ 1 0))]]) ]] [eval_id:=]
; = [[ (if [[([[#]] 10 10)]] #t [[(= 0 (/ 1 0))]]) ]] [eval_lit:#]
; = [[ (if [[ [[10]] = [[10]] ]] #t [[(= 0 (/ 1 0))]]) ]] [eval_lit:10]
; = [[ (if [[ 10 = [[10]] ]] #t [[(= 0 (/ 1 0))]]) ]] [eval_lit:10]
; = [[ (if [[ 10 = 10 ]] #t [[(= 0 (/ 1 0))]]) ]] [comparison]
; = [[ (if [[ #t ]] #t [[(= 0 (/ 1 0))]]) ]] [eval_lit:#t]
; = [[ (if #t #t [[(= 0 (/ 1 0))]]) ]] [apply]
; = [[ (if #t #t [[([[=]] 0 (/ 1 0))]]) ]] [eval_id:=]
; = [[ (if #t #t [[([[#]] 0 (/ 1 0))]]) ]] [eval_lit:#]
; = [[ (if #t #t [[(# 0 (/ 1 0))]]) ]] [apply_prim]
; = [[ (if #t #t [[ [[0]] = [[(/ 1 0)]] ]]) ]] [eval_lit:0]
; = [[ (if #t #t [[ 0 = [[(/ 1 0)]] ]]) ]] [apply]
; = [[ (if #t #t [[ 0 = [[([[/]] 1 0)]] ]]) ]] [eval_id:/]
; = [[ (if #t #t [[ 0 = [[([[#