Instructions
Objective
Write a Scheme assignment program to simulate the bit adder implementation using the knowledge of logic gates simulation.
Requirements and Specifications
Logic gates and adder are basic components of building a computer and any digital devices. All high-level language programs will be translated into instructions that can be executed on these basic components. The correctness and performance of these components are extremely important.
A computer system consists of hardware and software. Before we implement a hardware component, the design is normally simulated by a program first, so that we can verify its correctness and evaluate its performance. In this project, you will write Scheme programs to simulate an n-bit Adder.
Write three Scheme procedures to simulate these three gates (functions): AND, OR, and XOR, shown in the diagram in Figure 1. Test your procedures using all possible input combinations.
Screenshots of output
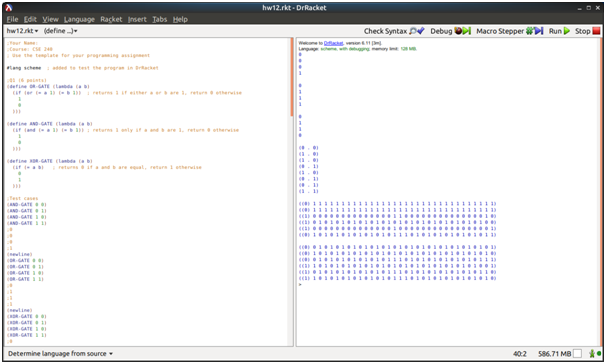
Source Code
;Your Name:
;Course: CSE 240
; Use the template for your programming assignment
#lang scheme ; added to test the program in DrRacket
;Q1 (6 points)
(define OR-GATE (lambda (a b)
(if (or (= a 1) (= b 1)) ; returns 1 if either a or b are 1, return 0 otherwise
1
0
)))
(define AND-GATE (lambda (a b)
(if (and (= a 1) (= b 1)) ; returns 1 only if a and b are 1, return 0 otherwise
1
0
)))
(define XOR-GATE (lambda (a b)
(if (= a b) ; returns 0 if a and b are equal, return 1 otherwise
0
1
)))
;Test cases
(AND-GATE 0 0)
(AND-GATE 0 1)
(AND-GATE 1 0)
(AND-GATE 1 1)
;0
;0
;0
;1
(newline)
(OR-GATE 0 0)
(OR-GATE 0 1)
(OR-GATE 1 0)
(OR-GATE 1 1)
;0
;1
;1
;1
(newline)
(XOR-GATE 0 0)
(XOR-GATE 0 1)
(XOR-GATE 1 0)
(XOR-GATE 1 1)
;0
;1
;1
;0
;Q2
(define bitAdder (lambda (x a b) ;(4 points each)
(cons (sum-bits x a b) (carry-out x a b)))) ; make list with sum and carry
(define sum-bits (lambda (x a b) ;(5 points each)
(XOR-GATE (XOR-GATE a b) x)))
(define carry-out (lambda (x a b) ;(5 points each)
(OR-GATE (AND-GATE (XOR-GATE a b) x) (AND-GATE a b))))
;Test cases
(newline)
(bitAdder 0 0 0)
(bitAdder 0 0 1)
(bitAdder 0 1 0)
(bitAdder 0 1 1)
(bitAdder 1 0 0)
(bitAdder 1 0 1)
(bitAdder 1 1 0)
(bitAdder 1 1 1)
;(0 . 0)
;(1 . 0)
;(1 . 0)
;(0 . 1)
;(1 . 0)
;(0 . 1)
;(0 . 1)
;(1 . 1)
;Q3.1 (4 points)
(define tail (lambda (lst)
(if (null? (cdr lst)) ; if we have empty tail we are at the last element
(car lst) ; return the last element
; else list remainder is not empty, recurse using list remainder
(tail (cdr lst)))))
;Q3.2 (4 points)
(define rmtail (lambda (lst)
(if (null? (cdr lst)) ; if we have empty tail we are at the last element
'() ; return empty list to remove the last element
; else list remainder is not empty, recurse using list remainder,
; keep the current element in the list
(cons (car lst) (rmtail (cdr lst))))))
;Q3.3 (4 points)
;(1) size-n is the number of bits to sum, the size-n problem will be finding the
; recursive procedure n-bit-adder1 that takes 2 n-bit binary numbers
; (lists of n elements), the n and the previous result (resulti) and returns
; the sum of n-bits and a carry-out
;(2) Stopping condition is n = 0, we added all bits, we return the sum and the
; carry-out of all previous bits which is passed in resulti
;(3) The size-(n-1) problem removes the last bit in each list and decrements n:
; (n-bit-adder (rmtail L1) (rmtail L2) (- n 1))
;(4) To build the size-n problem from size-(n-1), first we test the stopping
; condition, if test is true then we return the previous resulti
; if false, we recurse to the recursive size-(n-1) problem passing as resulti
; the sum of the current bits appended to the previous sum bit list and
; the previous carry.
;Q3.4 (14 points)
(define X1 '(0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0) )
(define X2 '(1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1) )
(define X3 '(0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1) )
(define X4 '(1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0) )
(define X5 '(0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1) )
(define X6 '(1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1) )
(define n-bit-adder1 (lambda (L1 L2 n)
; use helper to calculate sum, start with a carry-in of 0 and an empty list
(n-bit-adderhelper1 L1 L2 n '((0))) ))
(define n-bit-adderhelper1 (lambda (L1 L2 n resulti)
(if (= n 0) ; if stopping condition
resulti ; return previous result
; calculate the sum of the current bits and the previous carry,
; label result as sum, (car sum) will be the sum and (cdr sum) will be the carry
(let ((sum (bitAdder (tail L1) (tail L2) (caar resulti))))
; recurse removing the tail of the lists and decrementing n
(n-bit-adderhelper1
(rmtail L1)
(rmtail L2)
(- n 1)
; pass the current result as a list of a list containing only the carry
; and a list of the previous sums appending the current result at the start
(cons (list (cdr sum)) (cons (car sum) (cdr resulti))))))))
; this definition was not used but it calculates the carry for the n-bit sum
(define n-bit-adder-carry-out (lambda (L1 L2 n resulti)
(if (= n 0) ; if stopping condition
resulti ; return previous result
; else, recurse removing the tail of the lists and decrementing n
(n-bit-adder-carry-out
(rmtail L1)
(rmtail L2)
(- n 1)
; calculate the carry between the current bits and the previous result,
; pass the carry result on the recursive call as the resulti
(carry-out resulti (tail L1) (tail L2))))))
;Test cases
(newline)
(n-bit-adder1 X1 X2 32)
(n-bit-adder1 X3 X4 32)
(n-bit-adder1 X5 X6 32)
(n-bit-adder1 X2 X3 32)
(n-bit-adder1 X4 X5 32)
(n-bit-adder1 X1 X6 32)
(newline)
(n-bit-adder1 X1 X3 32)
(n-bit-adder1 X1 X4 32)
(n-bit-adder1 X1 X5 32)
(n-bit-adder1 X2 X4 32)
(n-bit-adder1 X2 X5 32)
(n-bit-adder1 X2 X6 32)
;((0) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1)
;((0) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1)
;((1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0)
;((1) 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0)
;((1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1)
;((0) 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1)
;((0) 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1)
;((0) 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0)
;((0) 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1)
;((1) 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1)
;((1) 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0)
;((1) 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0)