Instructions
Objective
Write an x86 assignment program to create a GCD routine in x86 assembly language, using recursive algorithm.
Requirements and Specifications
The greatest common divisor (GCD of two positive integers m and n can be calculated recursively by the function described below in pseudocode. function GCD(m, n : integer) : integer; if n = 0 then return m; else Remainder : = m mod n;
return GCD(n, Remainder);end if;
Implement this recursive definition in assembly language. Use the stack to pass the two doubleword-size argument values. Return the value of the function in the EAX register. The procedure should remove the parameters from the stack. Test your function with a main program that inputs two integers, calls the greatest common divisor function CD, and displays the value returned.
Program Specification:
Basic I/O (using io.h)
- Obtaining user input
- Using an input file
- Displaying computation results
Data Types
- WORD
Basic Instructions and Computations
- mov
- cmp
- div
- mul
- push
- рор
Write procedures
- main procedure
- GCD procedure
Screenshots of output
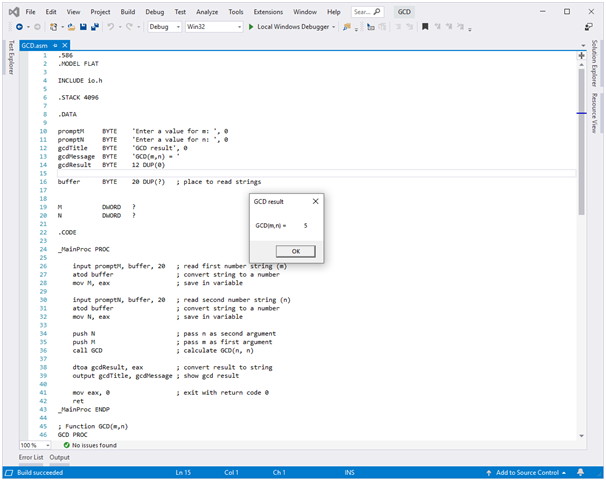
Source Code
.586
.MODEL FLAT
INCLUDE io.h
.STACK 4096
.DATA
promptM BYTE 'Enter a value for m: ', 0
promptN BYTE 'Enter a value for n: ', 0
gcdTitle BYTE 'GCD result', 0
gcdMessage BYTE 'GCD(m,n) = '
gcdResult BYTE 12 DUP(0) ; place to save result string
buffer BYTE 20 DUP(?) ; place to read strings
M DWORD ?
N DWORD ?
.CODE
_MainProc PROC
input promptM, buffer, 20 ; read first number string (m)
atod buffer ; convert string to a number
mov M, eax ; save in variable
input promptN, buffer, 20 ; read second number string (n)
atod buffer ; convert string to a number
mov N, eax ; save in variable
push N ; pass n as second argument
push M ; pass m as first argument
call GCD ; calculate GCD(n, n)
dtoa gcdResult, eax ; convert result to string
output gcdTitle, gcdMessage ; show gcd result
mov eax, 0 ; exit with return code 0
ret
_MainProc ENDP
; Function GCD(m,n)
GCD PROC
push ebp ; save frame pointer
mov ebp, esp ; point to top of stack
push ebx ; save EBX
mov eax, [ebp + 8] ; load first argument (m)
mov ebx, [ebp + 12] ; load second argument (n)
_if:
cmp ebx, 0 ; if n == 0
je _return ; return m (is already in eax)
_else:
mov edx, 0 ; clear edx to make division
div ebx ; divide m/n
push edx ; pass remainder as second argument
push ebx ; pass n as first argument
call GCD ; recurse GCD(n, remainder)
_return:
pop ebx ; restore EBX
pop ebp ; restore frame pointer
ret 8 ; return and remove arguments from stack
GCD ENDP
END ; end of source code