Instructions
Objective
Write a racket assignment program to create a BST tree.
Requirements and Specifications
Write a recursive function that finds a zero of a polynomial using the false position method.
The function takes 3 parameters: The polynomial function and two starting values.
Test this function with the two following polynomials:
For the function 9x2 - 3x - 25, you can use starting values 0 and 4:
Which evaluate to -25 and 107 respectively
You can assume that the two starting x values evaluate to y values that are on opposite sides of the x axis. (i.e. one y value is positive, the other negative)
For the function y = 11x2 - 2x – 50, you can use starting values -5 and 1:
Which evaluate to 235 and -41 respectively
Print out the final x value.
Helpful subfunctions:
a subfunction to decide if the current y value is accurate enough. The accuracy can be hard coded (0.001 or 0.0001 or so) or can be a parameter.
a subfunction that calculates the x intercept of a line segment given two endpoints.
Screenshots of output
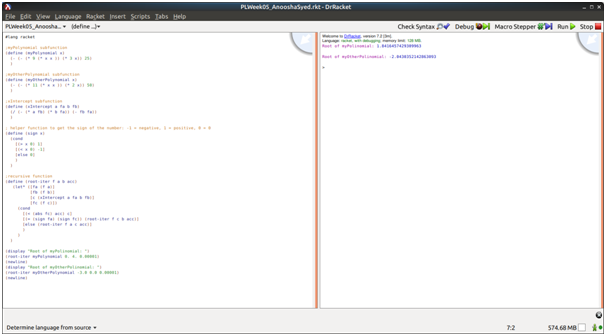
Source Code
#lang racket
;myPolynomial subfunction
(define (myPolynomial x)
(- (- (* 9 (* x x )) (* 3 x)) 25)
)
;myOtherPolynomial subfunction
(define (myOtherPolynomial x)
(- (- (* 11 (* x x )) (* 2 x)) 50)
)
;xIntercept subfunction
(define (xIntercept a fa b fb)
(/ (- (* a fb) (* b fa)) (- fb fa))
)
; helper function to get the sign of the number: -1 = negative, 1 = positive, 0 = 0
(define (sign x)
(cond
[(> x 0) 1]
[(< x 0) -1]
[else 0]
)
)
;recursive function
(define (root-iter f a b acc)
(let* ([fa (f a)]
[fb (f b)]
[c (xIntercept a fa b fb)]
[fc (f c)])
(cond
[(< (abs fc) acc) c]
[(= (sign fa) (sign fc)) (root-iter f c b acc)]
[else (root-iter f a c acc)]
)
)
)
(display "Root of myPolinomial: ")
(root-iter myPolynomial 0. 4. 0.00001)
(newline)
(display "Root of myOtherPolinomial: ")
(root-iter myOtherPolynomial -3.0 0.0 0.00001)
(newline)