(1).Consider the grammar in Figure 1 where the terminal int denotes an integer and the terminal id
S → Atoms
Atoms → ϵ
Atoms → Atom Atoms Atom → J Atom
Atom → id
Atom→ int
Atom→ ( Atoms )
Figure 1: A simplified grammar for Scheme.
denotes an identifier. The only other terminals in this grammar are the quote ’, the left parenthesis
(, and the right parenthesis ).
The scheme, a derivative of Lisp, is a list-based language where all programs are represented by lists. For example, a simple Scheme program
( + 1 2 )
adds two numbers together and prints out the result. A scheme interpreter, /local/bin/scheme, is available on timberlea.cs.dal.ca. Feel free to give it a try. Write a LISP assignment program, where is zero or more atoms is executed by evaluating each of the atoms. An atom is either an integer, an identifier, or a list. The evaluation of an integer is the integer, and the evaluation of an identifier, for now, is simply the identifier. The evaluation of a quoted atom is simply the atom itself. E.g., the evaluation of ’ ( 1 2 3 ) is ( 1 2 3 ).
A list is evaluated by evaluating the first atom of the list and treating the result as a function. Then each of the remaining atoms of the list is evaluated and passed as parameters to the function. For example, the evaluation of ( + 1 2 ), treats + as a function, and passes 1 and 2 to the function. Applying + to 1 and 2 yields result 3. Whereas, the evaluation of ( + 1 ( * 2 3 ) ), evaluates + and 1 as before, but then evaluates ( * 2 3 ), yielding 6, which is then passed to the + function, which yields the result of 7.
- Consider the following L-attributed grammar, based on the grammar specified in Figure 1. Describe and justify what it is computing. Be sure to explain the purpose of the attributes, and what each of the semantic rules is doing. Your description must include a succinct summary of the purpose of this attribute grammar.
| Symbol | Attribute | Type |
| Atoms | calls: int callable: bool symbol table: Symbol Table | Synthesized Synthesized Inherited |
| Atom | calls: int callable: bool symbol table: Symbol Table | Synthesized Synthesized Inherited |
In the attribute grammar below, the symbol D indicates a semantic rule that operates on inherited attributes, and the symbol indicates a semantic rule that operates on synthesized attributes.
S → Atoms1 D Atoms1.symbol table = getSymbolTable()
print (Atoms1.calls)
Atoms → ϵ Atoms.calls = 0
Atoms.callable = false
Atoms → Atom1 Atoms1 D Atom1.symbol table = Atoms.symbol table
D Atoms1.symbol table = Atoms.symbol table
Atoms.calls = Atom1.calls + Atoms1.calls
Atoms.callable = Atom1.callable
Atom → J Atom1 D Atom1.symbol table = Atom.symbol table
Atom.calls = 0
Atom.callable = false
Atom → id Atom.calls = 0
Atom.callable = Atom.symbol table.isFunction(id) Atom → int Atom.calls = 0
Atom.callable = false
Atom → ( Atoms1 ) D Atoms1.symbol table = Atom.symbol table
if Atoms1.callable then Atom.calls = Atoms1.calls + 1
Atom.callable = Atoms1.callable
To begin, I want to mention that this grammar is not ambiguous since there is only one way to extend the provided nonterminal in order to generate the right derivation at any point in the parse.
Mainly, This L-attributed grammar is doing exactly what was expected from it to do in the above description:
To begin, I want to mention that this grammar is not ambiguous since there is only one way to extend the provided nonterminal in order to generate the right derivation at any point in the parse.
Mainly, This L-attributed grammar is doing exactly what was expected from it to do in the above description:
- A quoted atom's evaluation is simply the atom itself. For example, the evaluation of'( 1 2 3 ) is ( 1 2 3 ).
- When evaluating a list, the first atom is evaluated and the result is treated as a function. The remaining atoms in the list are then evaluated and provided as arguments for the function. For example, in the evaluation of ( + 1 2 ), + is treated as a function, and 1 and 2 are sent to the function.
- When + is applied to 1 and 2, the result is 3. In contrast, the evaluation of ( + 1 ( * 2 3 ) ), evaluates + and 1 as before, but then evaluates ( * 2 3
), producing 6, which is then given to the + function, yielding 7.
Moreover, the goal from each semantic rule is:
- Go to the Symbol Table and bring the type and the value of the (Atom or Atoms).
- Verify if it’s callable or not.
- Compute the value, type, and callability of the new expression then put it in the Symbol Table.
Furthermore, the purpose of the attributes Atom and Atoms:
- Atom: it's for a simple expression. In our case, it used to add two numbers together and for the quoted one.
- Atoms: it' is for complex expression. In our case, It used to handle a list (the rest of the expression).
In conclusion, the purpose of this L-attributed grammar is to evaluate a prefix
expression and print out the result.
2. Suppose you wanted to construct an abstract syntax tree from parse tree derived by using the grammar specified in Figure 1. Give an S-attributed grammar that creates an abstract syntax tree composed of the following kinds of tree nodes as illustrated in the UML diagram below.
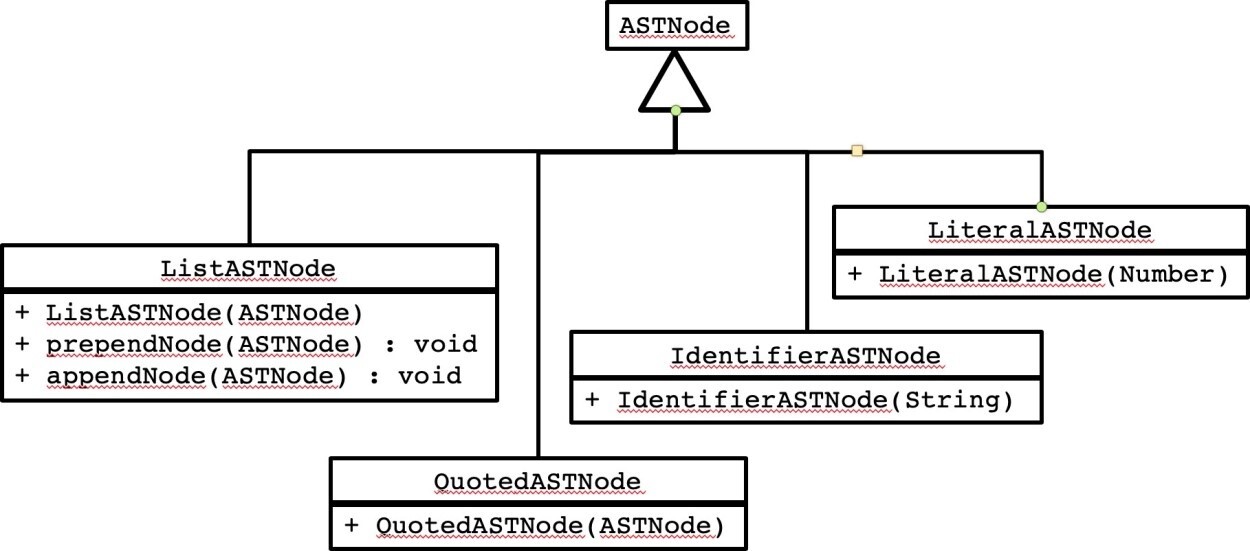
All that is required is to create an abstract syntax tree. Observe that all you will need for most types of nodes is just the constructor (as shown) but for ListASTNode two methods are provided to prepend and append nodes to a list. You will need one of these methods, depending on how you structure your attribute grammar.
Please provide both the semantic rules and the attributes using notation similar to that in question 1.
To create an Abstract Syntax Tree (AST), we will add these modifications:
- for these rules

we will use this:

we will end up with:
- Atoms1.ListAsnode()
- Atoms1.prependNode()
- Atoms1.appendNode()
2. for this rule
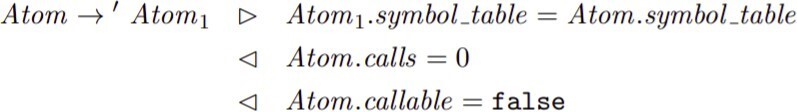
we will use this:
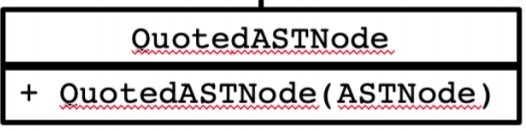
we will end up with:
- Atom.QuotedASTNode()
3. for this rule:
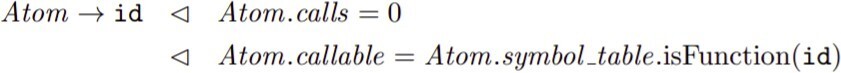
we will use this: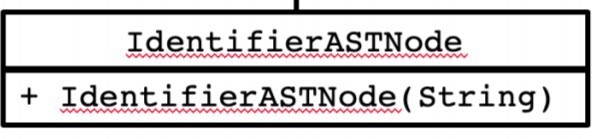
we will end up with:
- Atom.IdentifierASTNode()
4. for this rule:
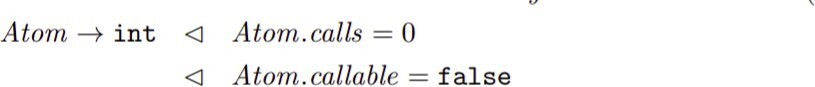
we will use this:

we will end up with:
- Atom.LiteralASTNode()
5. for this rule
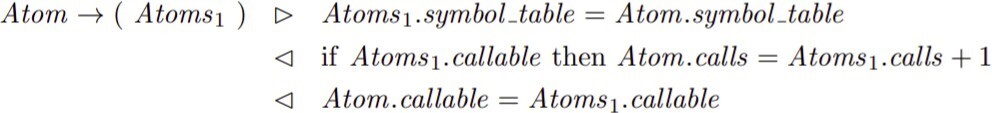
we will use:

Creating an AST for the example that was provided in question 1. the AST for this expression ( + 1 ( * 2 3 ) ) will be:
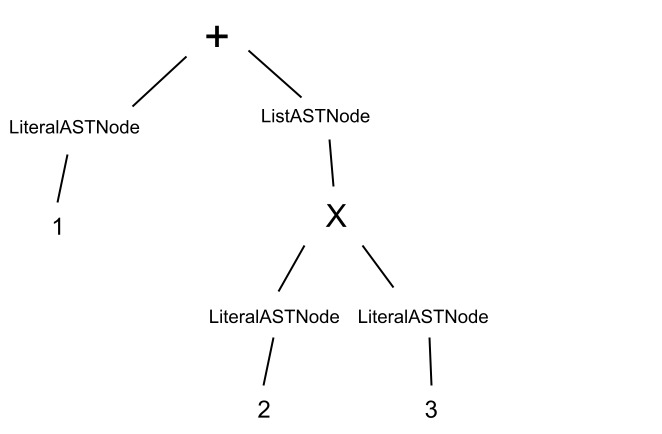
To achieve this AST we used the following the flowing rules:
1.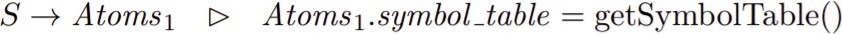
2.

3.
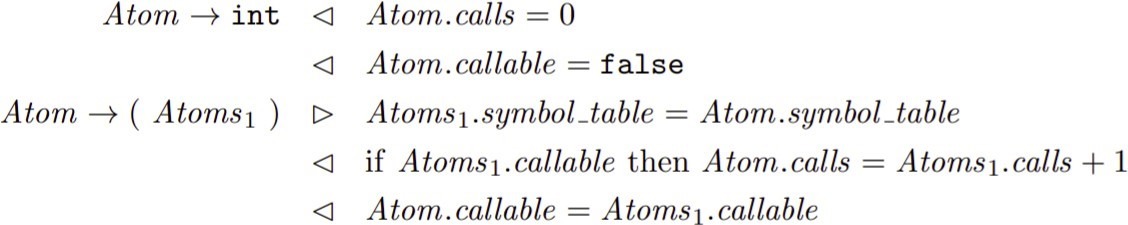
3. Suppose that the base ASTNode class had a setPosition(int n) method that sets the position of the node in the abstract syntax tree. The position is location of the symbol in its inner most list. E.g., for ((a) b (c d) e) the position of atom (a) is 0, the position of atom b is 1, the position of atom atom (c d) is 2, the position of atom c is 0, the position of atom d is 1, and the position of atom e is 3.
Extend the S-attributed grammar from Question 2 into an L-attributed grammar that also sets the position of each node in the abstract syntax tree as it is created.
Provide a brief explanation of how the grammar works.
To extend the S-attributed grammar from Question 2 into an L-attributed grammar that also sets the position of each node in the abstract syntax tree,
we only need to add the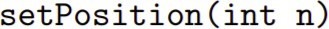 in these two
in these two
sections 2.3 and 2.4.
the end result will be something like this:
- Atom.LiteralASTNode().setPostion( int n)
- Atom.IdentifierASTNode().setPostion( int n)
Where n: needs to be calculated with a routine that looks like this.
