Instructions
Objective
Write a program to operate on sets using Haskell language.
Requirements and Specifications
Ordered Lists for Sets
To complete the Haskell assignment, we use lists to represent sets. Element types are instances of Ord; each list has elements in strictly increasing order. A list may be infinite, representing an infinite set. We can still perform some set operations meaningfully on infinite lists because the elements are in strictly increasing order.
Implement unioning of two sets. Sine the inputs are sorted lists, this is like the merge stage in mergesort, except: If an element occurs in both input lists, “set union” means you want only one occurrence in the output list.
union :: Ord a => [a] -> [a] -> [a]
In this question, you will implement a function that generates this set in our list representation:
{f u v | u ∈ xs, v ∈ ys}
To be sure, this would be very difficult or impossible for infinite sets if f is arbitrary. But it is very doable (even efficient) if we require f to be strictly monotonic; more precisely:
- If x < x′, then f x y < f x′ y
- If y < y′, then f x y < f x y′
The following idea suggests an algorithm. I leave the base cases (when xs or ys is empty) to you. But if
- xs has least element x (the 1st element in the list form), and the remaining elements are xt
- ys has least element y, and the remaining elements are yt then this decomposition is helpful:
{f u v | u ∈ xs, v ∈ ys} = {f x y} ∪ {f x v | v ∈ yt} ∪ {f u v | u ∈ xt, v ∈ ys}
Note:
- f x y is the least element of the output set, so you already know that it must be the 1st element of the output list.
- The 3rd component can be done by a recursive call.
- Although the formula uses ∪ twice, it is not a good idea to use union for both! (You can try and run into a problem). What is the first bullet point suggesting?
Implement this as the function setBinOp:
setBinOp :: (Ord a, Ord b, Ord c) => (a -> b -> c) -> [a] -> [b] -> [c]
setBinOp f xs ys is the list representation for {f u v | u ∈ xs, v ∈ ys}.
For example, if we have the powers of 2 and the powers of 3 in increasing order:
powers2 = iterate (* 2) 1
powers3 = iterate (* 3) 1
Then setBinOp (*) powers2 powers3 is the list of all numbers of the form 2i × 3j in increasing order.
We now set up a binary tree type that stores tree sizes. This will be used in the next question in which we work with a list of trees in increasing sizes.
Here are the definitions of the tree type and a wrapper type that stores a tree and its size. We use the number of leaf nodes (L) as size.
data BinaryTree = L | B BinaryTree BinaryTree deriving (Eq, Ord, Show)
data SizedTree = S Integer BinaryTree deriving (Eq, Ord, Show)
Implement:
- leaf :: SizedTree (a leaf and its size).
- branch :: SizedTree -> SizedTree -> SizedTree
that builds a new tree using the two input trees as children (left child is 1st argument), and computes and stores the new size.
Notice that SizedTree derives Ord; the auto-generated order compares by size first (simply because that’s the 1st field). This is playing well with our plan of working with a list of increasing tree sizes!
We note that the set S of all sized trees satisfies this recursive equation:
S = {leaf } ∪ {branch t1 t2 | t1 ∈ S, t2 ∈ S}
Implement S as allSizedTrees :: [SizedTree].
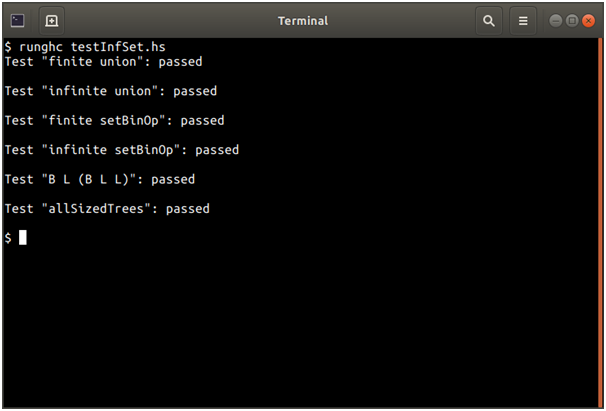
Screenshots of output
Source Code
module InfSet where
import InfSetDefunion :: Ord a => [a] -> [a] -> [a]
union xs [] = xs
union [] ys = ys
union xs@(x:xt) ys@(y:yt)
| x < y = x : union xt ys
| y < x = y : union xs yt
| otherwise = x : union xt yt
setBinOp :: (Ord a, Ord b, Ord c) => (a -> b -> c) -> [a] -> [b] -> [c]
setBinOp f _ [] = []
setBinOp f [] _ = []
setBinOp f (x:xt) ys@(y:yt) = f x y : union [f x y' | y' <- yt] (setBinOp f xt ys)
leaf :: SizedTree
leaf = S 1 L
branch :: SizedTree -> SizedTree -> SizedTree
branch (S i lt) (S j rt) = S (i + j) (B lt rt)
allSizedTrees :: [SizedTree]
allSizedTrees = leaf : setBinOp branch allSizedTrees allSizedTrees