Instructions
Objective
Write a Haskell assignment program that allows users to evaluate mathematical expressions.
Requirements and Specifications
1. Write a function eval that takes an environment and an expression and evaluates
-- the expression. The environment is a list of (name, value) pairs. Use lookup to obtain
-- the value for a variable. If the variable is not defined in the environment (meaning
-- lookup returns Nothing), use 0.
-- 2. Write a function meval that takes an environment and an expression and evaluates
-- the expression. If the expression refers to any variables not defined in the
-- environment, it returns Nothing.
-- 3. Write a function peval that partially evaluates an expression, given a context.
-- For our purposes, partial evaluation will
-- 1. replace any variable defined in the environment with its value
-- 2. perform any operation when neither operand contains a variable
-- 3. simplify 0 + x, x + 0, x - 0, x * 1, 1 * x, x * 0, 0 * x
Screenshots of output
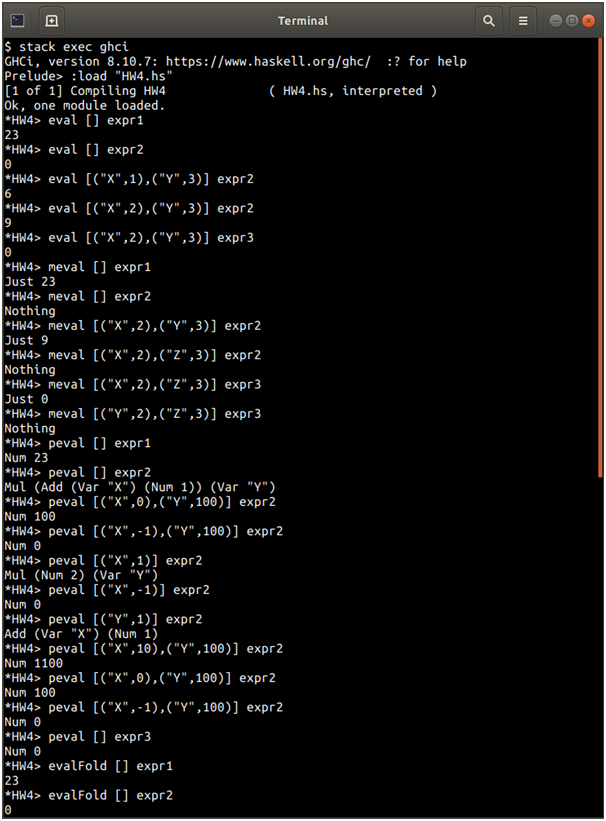
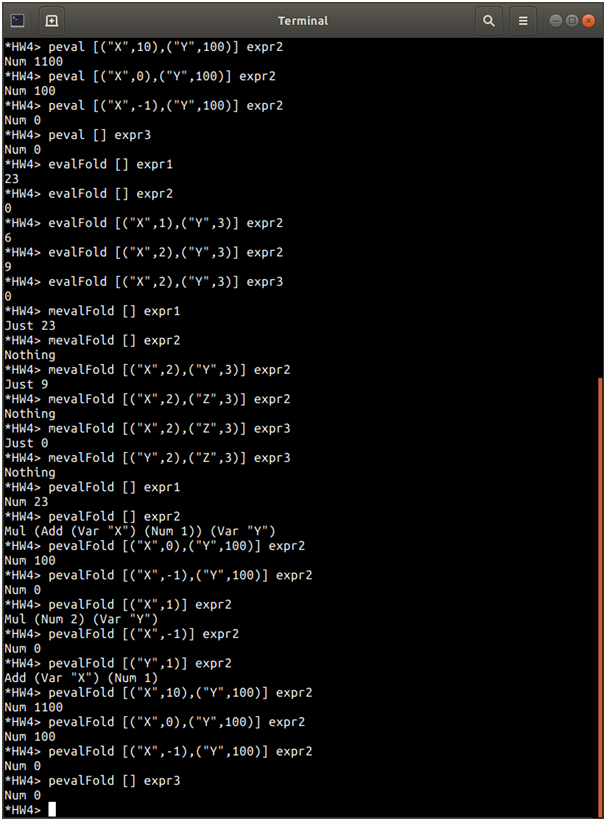
Source Code
module HW4 where
import Data.List (lookup)
import Control.Applicative (liftA2)
data Expr
= Var String
| Num Integer
| Add Expr Expr
| Sub Expr Expr
| Mul Expr Expr
deriving (Show)
-- 3 + 4 * 5
expr1 = Add (Num 3) (Mul (Num 4) (Num 5))
-- (X + 1) * Y
expr2 = Mul (Add (Var "X") (Num 1)) (Var "Y")
-- (1 + (-1)) * X
expr3 = Mul (Add (Num 1) (Num (-1))) (Var "X")
-- ****
-- 1. Write a function eval that takes an environment and an expression and evaluates
-- the expression. The environment is a list of (name, value) pairs. Use lookup to obtain
-- the value for a variable. If the variable is not defined in the environment (meaning
-- lookup returns Nothing), use 0.
--
-- *HW4> eval [] expr1
-- 23
-- *HW4> eval [] expr2
-- 0
-- *HW4> eval [("X",1),("Y",3)] expr2
-- 6
-- *HW4> eval [("X",2),("Y",3)] expr2
-- 9
-- *HW4> eval [("X",2),("Y",3)] expr3
-- 0
--
-- Note: the environment may include variables not used in the expression. You may assume
-- that the environment does not include multiple definitions for one variable.
eval :: [(String, Integer)] -> Expr -> Integer
eval env (Var ss) = case lookup ss env of
Just x -> x
Nothing -> 0
eval env (Num n) = n
eval env (Add e1 e2) = eval env e1 + eval env e2
eval env (Sub e1 e2) = eval env e1 - eval env e2
eval env (Mul e1 e2) = eval env e1 * eval env e2
-- ****
-- 2. Write a function meval that takes an environment and an expression and evaluates
-- the expression. If the expression refers to any variables not defined in the
-- environment, it returns Nothing.
--
-- *HW4> meval [] expr1
-- Just 23
-- *HW4> meval [] expr2
-- Nothing
-- *HW4> meval [("X",2),("Y",3)] expr2
-- Just 9
-- *HW4> meval [("X",2),("Z",3)] expr2
-- Nothing
-- *HW4> meval [("X",2),("Z",3)] expr3
-- Just 0
-- *HW4> meval [("Y",2),("Z",3)] expr3
-- Nothing
--
-- Hint: Maybe is an instance of Applicative, meaning it can be used with liftA2.
-- Experiment with liftA2 f a b, where f :: Integer -> Integer -> Integer and
-- a, b :: Maybe Integer. If used correctly, this can significantly simplify your code.
meval :: [(String, Integer)] -> Expr -> Maybe Integer
meval env (Var ss) = lookup ss env
meval env (Num n) = Just n
meval env (Add e1 e2) = liftA2 (+) (meval env e1) (meval env e2)
meval env (Sub e1 e2) = liftA2 (-) (meval env e1) (meval env e2)
meval env (Mul e1 e2) = liftA2 (*) (meval env e1) (meval env e2)
-- ****
-- 3. Write a function peval that partially evaluates an expression, given a context.
-- For our purposes, partial evaluation will
-- 1. replace any variable defined in the environment with its value
-- 2. perform any operation when neither operand contains a variable
-- 3. simplify 0 + x, x + 0, x - 0, x * 1, 1 * x, x * 0, 0 * x
--
-- peval is not required to handle every possible simplification. For example, x - x
-- can be left as-is.
-- *HW4> peval [] expr1
-- Num 23
-- *HW4> peval [] expr2
-- Mul (Add (Var "X") (Num 1)) (Var "Y")
-- *HW4> peval [("X",0),("Y",100)] expr2
-- Num 100
-- *HW4> peval [("X",-1),("Y",100)] expr2
-- Num 0
-- *HW4> peval [("X",1)] expr2
-- Mul (Num 2) (Var "Y")
-- *HW4> peval [("X",-1)] expr2
-- Num 0
-- *HW4> peval [("Y",1)] expr2
-- Add (Var "X") (Num 1)
-- *HW4> peval [("X",10),("Y",100)] expr2
-- Num 1100
-- *HW4> peval [("X",0),("Y",100)] expr2
-- Num 100
-- *HW4> peval [("X",-1),("Y",100)] expr2
-- Num 0
-- *HW4> peval [] expr3
-- Num 0
--
-- Suggestion: write non-recursive helper functions that take the arguments for Add, Sub,
-- or Mul, and handle the cases where both arguments are Num, or where one argument is
-- Num 0 or Num 1.
peval :: [(String, Integer)] -> Expr -> Expr
peval env (Var ss) = case lookup ss env of
Just x -> Num x
Nothing -> Var ss
peval env (Num n) = Num n
peval env (Add e1 e2) = phelper '+' (peval env e1) (peval env e2)
peval env (Sub e1 e2) = phelper '-' (peval env e1) (peval env e2)
peval env (Mul e1 e2) = phelper '*' (peval env e1) (peval env e2)
-- simplifies nums, 0 + x, x + 0, x - 0, x * 1, 1 * x, x * 0, 0 * x
-- leaves everything as expr
phelper :: Char -> Expr -> Expr -> Expr
phelper '+' (Num a) (Num b) = Num (a + b)
phelper '-' (Num a) (Num b) = Num (a - b)
phelper '*' (Num a) (Num b) = Num (a * b)
phelper '+' (Num 0) (Var x) = Var x
phelper '+' e1 (Num 0) = e1
phelper '-' e1 (Num 0) = e1
phelper '*' e1 (Num 1) = e1
phelper '*' (Num 1) e2 = e2
phelper '*' e1 (Num 0) = Num 0
phelper '*' (Num 0) e2 = Num 0
phelper '+' e1 e2 = Add e1 e2
phelper '-' e1 e2 = Sub e1 e2
phelper '*' e1 e2 = Mul e1 e2
-- ****
-- Extra credit: all three of the above functions could be written succinctly as folds
-- over the Expr type. Write a generic fold function and then implement eval, meval, and
-- peval using it.
--
-- You will need to determine the number of base cases and combining functions required.
-- The most natural way to write foldExpr will require more than one of each.
foldExpr :: (a -> a -> a) -> (a -> a -> a) -> (a -> a -> a) -> (Integer -> a) -> (String -> a) -> Expr -> a
foldExpr fa fs fm fn fv (Var ss) = fv ss
foldExpr fa fs fm fn fv (Num n) = fn n
foldExpr fa fs fm fn fv (Add e1 e2) = fa (foldExpr fa fs fm fn fv e1) (foldExpr fa fs fm fn fv e2)
foldExpr fa fs fm fn fv (Sub e1 e2) = fs (foldExpr fa fs fm fn fv e1) (foldExpr fa fs fm fn fv e2)
foldExpr fa fs fm fn fv (Mul e1 e2) = fm (foldExpr fa fs fm fn fv e1) (foldExpr fa fs fm fn fv e2)
evalFold :: [(String, Integer)] -> Expr -> Integer
evalFold env expr = foldExpr (+) (-) (*) id fv expr
where fv ss = case lookup ss env of
Just x -> x
Nothing -> 0
mevalFold :: [(String, Integer)] -> Expr -> Maybe Integer
mevalFold env expr = foldExpr (liftA2 (+)) (liftA2 (-)) (liftA2 (*)) Just (`lookup` env) expr
pevalFold :: [(String, Integer)] -> Expr -> Expr
pevalFold env expr = foldExpr (phelper '+') (phelper '-') (phelper '*') Num fv expr
where fv ss = case lookup ss env of
Just x -> Num x
Nothing -> Var ss