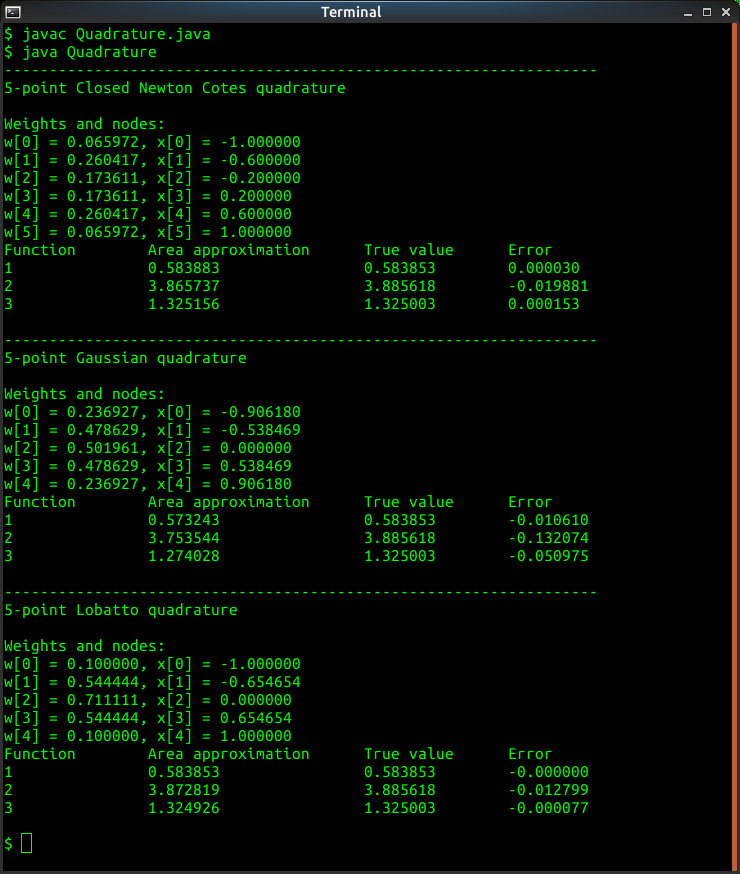
Quadrature Results, Weights, and Nodes
/*
* PURPOSE: Evaluatestheclosed Newton Cotes, Gaussian and Lobatto
* quadraturemethodsusing 3 differentfunctions, displaysthequadrature
* results, weights and nodesused
* OUTPUT: Printsallquadratureresultsonthescreen.
*/
publicclassQuadrature {
/**
* PURPOSE: Definitionofthefirstfunctionto use in thequadratures
* INPUT: x, position in X usedtoevaluatefunction
* OUTPUT: double, evaluationofthefirstfunction in X.
*/
publicstaticdouble function1(double x) {
return 1 - Math.sin(1 - x);
}
/**
* PURPOSE: Definitionofthesecondfunctionto use in thequadratures
* INPUT: x, position in X usedtoevaluatefunction
* OUTPUT: double, evaluationofthefirstfunction in X.
*/
publicstaticdouble function2(double x) {
returnMath.sqrt(x + 1) + 1;
}
/**
* PURPOSE: Definitionofthethirdfunctionto use in thequadratures
* INPUT: x, position in X usedtoevaluatefunction
* OUTPUT: double, evaluationofthefirstfunction in X.
*/
publicstaticdouble function3(double x) {
returnMath.tanh(x + 1);
}
/**
* PURPOSE: Evaluatethequadratureofthe 3 functionsdefinedaboveusing
* theclosed Newton Cotes quadrature
* INPUT: None
* OUTPUT: printsthequadratureresultsonthescreen.
*/
publicstaticvoidnewtonCotes() {
int n = 5; // use 5 points
double x0 = -1; // lowerlimit
doublexn = 1; // upperlimit
double h = (xn - x0)/n; // step size
double w [] = { // weights
19./288.,
25./96.,
25./144.,
25./144.,
25./96.,
19./288.
};
double x [] = new double[n+1]; // node positions
doublequadrature [] = {0.0, 0.0 ,0.0}; // itwillholdthequadratureresults
doubletrueArea[] = {
0.58385316345285761300, // true areaforfunction 1
3.8856180831641267317, // true areaforfunction 2
1.3250027473578644309 // true areaforfunction 3
};
// node positions
for (int i=0; i<=n; i++)
x[i] = x0 + i*h;
// Printweights and nodes
System.out.println("------------------------------------------------------------------");
System.out.println("5-point Closed Newton Cotes quadrature\n");
System.out.println("Weights and nodes:");
for (int i=0; i<=n; i++) {
System.out.printf("w[%d] = %f, x[%d] = %f\n", i, w[i], i, x[i]);
}
// Evaluatethequadratureoffirstfunctionusingthe 5-point rule
quadrature[0] = 0.0; // initializetozeroformakingthe sum
for (int i=0; i<=n; i++)
quadrature[0] += (xn - x0)*w[i]*function1(x[i]); //addnodecontributionto sum
// Evaluatethequadratureofsecondfunction
quadrature[1] = 0.0; // initializetozeroformakingthe sum
for (int i=0; i<=n; i++)
quadrature[1] += (xn - x0)*w[i]*function2(x[i]); //addnodecontributionto sum
// Evaluatethequadratureofthirdfunction
quadrature[2] = 0.0; // initializetozeroformakingthe sum
for (int i=0; i<=n; i++)
quadrature[2] += (xn - x0)*w[i]*function3(x[i]); //addnodecontributionto sum
System.out.println("Function\tAreaapproximation\tTruevalue\tError");
for (int i=0; i<3; i++) {
double error = quadrature[i] - trueArea[i];
System.out.printf("%d\t\t%f\t\t%f\t%f\n", i+1, quadrature[i], trueArea[i], error);
}
System.out.println();
}
/**
* PURPOSE: Evaluatethequadratureofthe 3 functionsdefinedaboveusing
* the Gaussian quadrature
* INPUT: None
* OUTPUT: printsthequadratureresultsonthescreen.
*/
publicstaticvoidgaussian() {
int n = 5; // use 5 points
double x0 = -1; // lowerlimit
doublexn = 1; // upperlimit
double w [] = { // weights
(322 - 13*Math.sqrt(70))/900.,
(322 + 13*Math.sqrt(70))/900.,
128./255.,
(322 + 13*Math.sqrt(70))/900.,
(322 - 13*Math.sqrt(70))/900.,
};
double x [] = { // node positions
-Math.sqrt(5 + 2*Math.sqrt(10./7.))/3.,
-Math.sqrt(5 - 2*Math.sqrt(10./7.))/3.,
0,
Math.sqrt(5 - 2*Math.sqrt(10./7.))/3.,
Math.sqrt(5 + 2*Math.sqrt(10./7.))/3.,
};
doublequadrature [] = {0.0, 0.0 ,0.0}; // itwillholdthequadratureresults
doubletrueArea[] = {
0.58385316345285761300, // true areaforfunction 1
3.8856180831641267317, // true areaforfunction 2
1.3250027473578644309 // true areaforfunction 3
};
// Printweights and nodes
System.out.println("------------------------------------------------------------------");
System.out.println("5-point Gaussian quadrature\n");
System.out.println("Weights and nodes:");
for (int i=0; i