Create Program to Solve Polynomial in Racket in Racket Assignment Solution

Instructions

Objective

Write a racket assignment program to create a BST tree.

Requirements and Specifications

Write a recursive function that finds a zero of a polynomial using the false position method.

The function takes 3 parameters: The polynomial function and two starting values.

Test this function with the two following polynomials:

For the function 9x2 - 3x - 25, you can use starting values 0 and 4:

Which evaluate to -25 and 107 respectively

You can assume that the two starting x values evaluate to y values that are on opposite sides of the x axis. (i.e. one y value is positive, the other negative)

For the function y = 11x2 - 2x – 50, you can use starting values -5 and 1:

Which evaluate to 235 and -41 respectively

Print out the final x value.

Helpful subfunctions:

a subfunction to decide if the current y value is accurate enough. The accuracy can be hard coded (0.001 or 0.0001 or so) or can be a parameter.

a subfunction that calculates the x-intercept of a line segment given two endpoints.

Screenshots of output

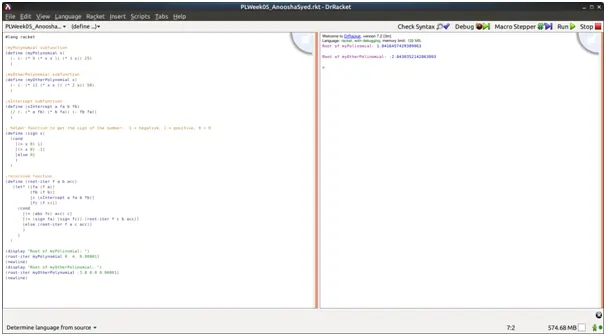
Source Code

#lang racket ;myPolynomial subfunction (define (myPolynomial x) (- (- (* 9 (* x x )) (* 3 x)) 25) ) ;myOtherPolynomial subfunction (define (myOtherPolynomial x) (- (- (* 11 (* x x )) (* 2 x)) 50) ) ;xIntercept subfunction (define (xIntercept a fa b fb) (/ (- (* a fb) (* b fa)) (- fb fa)) ) ; helper function to get the sign of the number: -1 = negative, 1 = positive, 0 = 0 (define (sign x) (cond [(> x 0) 1] [(< x 0) -1] [else 0] ) ) ;recursive function (define (root-iter f a b acc) (let* ([fa (f a)] [fb (f b)] [c (xIntercept a fa b fb)] [fc (f c)]) (cond [(< (abs fc) acc) c] [(= (sign fa) (sign fc)) (root-iter f c b acc)] [else (root-iter f a c acc)] ) ) ) (display "Root of myPolinomial: ") (root-iter myPolynomial 0. 4. 0.00001) (newline) (display "Root of myOtherPolinomial: ") (root-iter myOtherPolynomial -3.0 0.0 0.00001) (newline)