Program To Solve Fluid Questions in OOP Language Assignment Solution

Instructions

Objective

If you require assistance with your Object-Oriented Programming assignment, I can help you craft a program that tackles fluid questions using OOP concepts. The task involves writing a program that effectively addresses fluid-related problems while applying principles like encapsulation, inheritance, and polymorphism. By implementing these Object-Oriented Programming techniques, the program can efficiently model fluid scenarios and provide accurate solutions. Feel free to provide any specific requirements or guidelines for your assignment, and I'll ensure the code meets your needs while demonstrating a solid understanding of OOP principles.

Requirements and Specifications

Source Code

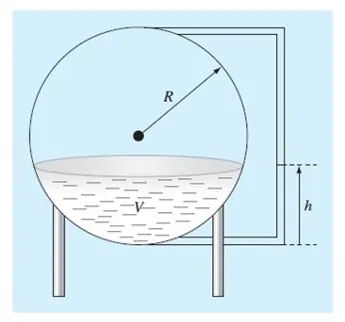
PROBLEM 1 clc, clear all, close all %% Parameters of the tank R = 3; %% We want to calculate the depth of the tank such that the volume is 30 m^3. So: % pi*h^2 *(3*R-h)/3 = 30 % Then, the function will be: % f(x) = pi*x^2 *(3*R-x)/3 - 30, where h = x f = @(x)(pi*x^2 *(3*R - x)/3 - 30); %% Pat a) Newton's Method % The first derivate of this function respect to x is: df = @(x)(2*x*pi*(3*R - x)/3 - pi*x^2 /3); % Define initial error and tolerance error = Inf; tol = 1e-6; % Define initial value x = R; n = 1; while error >= tol % execute algorithm while the error is higher than the tolerance x = x - f(x)/df(x); error = abs(f(x)); % fprintf("Iteration %d, error = %.8f\n", n, error); n = n + 1; end fprintf("The solution obtained using Newton's method in %d iterations is h = %.4f m\n", n, x); %% Part b): Secant Method %% Define the interval [a,b] in which we assume the solution may be a = 1; b = 3; % Define initial error and tolerance error = Inf; tol = 1e-6; max_iters = 500; n = 1; while error >= tol % execute algorithm while the error is higher than the tolerance x0 = a; x1 = b; x2 = x1 - (x1-x0)*f(x1) / (f(x1)-f(x0)); % calculate x2 aold = a; bold = b; % Update a = x1; b = x2; error = abs(b-a)/abs(a); %% Enable the following line if you want to check the error per iteration % fprintf("Iter = %d, aold = %.4f, bold = %.4f, x2 = %.4f, anew = %.4f, bnew = %.4f, error = %.8f\n", n, aold, bold, x2, a, b, error); % fprintf("Iteration %d, error: %.8f\n", n, error); % Increment step n = n + 1; % If the number if iterations reaches the max. number of iterations % allowed, it means that the problem did not find a solution if n >= max_iters break; end end fprintf("The solution obtained using Secant method in %d iterations is h = %.4f m\n", n, a); PROBLEM 2 clc, clear all, close all %% Define the equation of the specific heat % We assume T = x f = @(x)(1.1 - (0.99403 + 1.671e-4 *x + 9.7215e-8 *x^2 -9.5838e-11 *x^3 + 1.9520e-14 *x^4)); %% Pat a) Newton's Method % The first derivate of this function respect to x is: df = @(x)(-(1.671e-4 + 2*9.7215e-8 *x -3*9.5838e-11 *x^2 + 4*1.9520e-14 *x^3)); % Define initial error and tolerance error = Inf; tol = 1e-6; % Define initial value x = 150; % in kelvins n = 1; while error >= tol % execute algorithm while the error is higher than the tolerance x = x - f(x)/df(x); error = abs(f(x)); % fprintf("Iteration %d, error = %.8f\n", n, error); n = n + 1; end fprintf("The solution obtained using Newton's method in %d iterations is T = %.4f K\n", n, x); %% Part b): Secant Method %% Define the interval [a,b] in which we assume the solution may be a = 0; b = 1000; % Define initial error and tolerance error = Inf; tol = 1e-6; max_iters = 500; n = 1; while error >= tol % execute algorithm while the error is higher than the tolerance x0 = a; x1 = b; x2 = x1 - (x1-x0)*f(x1) / (f(x1)-f(x0)); % calculate x2 aold = a; bold = b; % Update a = x1; b = x2; error = abs(b-a)/abs(a); %% Enable the following line if you want to check the error per iteration % fprintf("Iter = %d, aold = %.4f, bold = %.4f, x2 = %.4f, anew = %.4f, bnew = %.4f, error = %.8f\n", n, aold, bold, x2, a, b, error); % fprintf("Iteration %d, error: %.8f\n", n, error); % Increment step n = n + 1; % If the number if iterations reaches the max. number of iterations % allowed, it means that the problem did not find a solution if n >= max_iters break; end end fprintf("The solution obtained using Secant method in %d iterations is T = %.4f K\n", n, a);