Add Lambda Expressions In Haskell Assignment Solution

Instructions

Objective

Write a program to add lambda add lambda expressions in haskel..

Requirements and Specifications

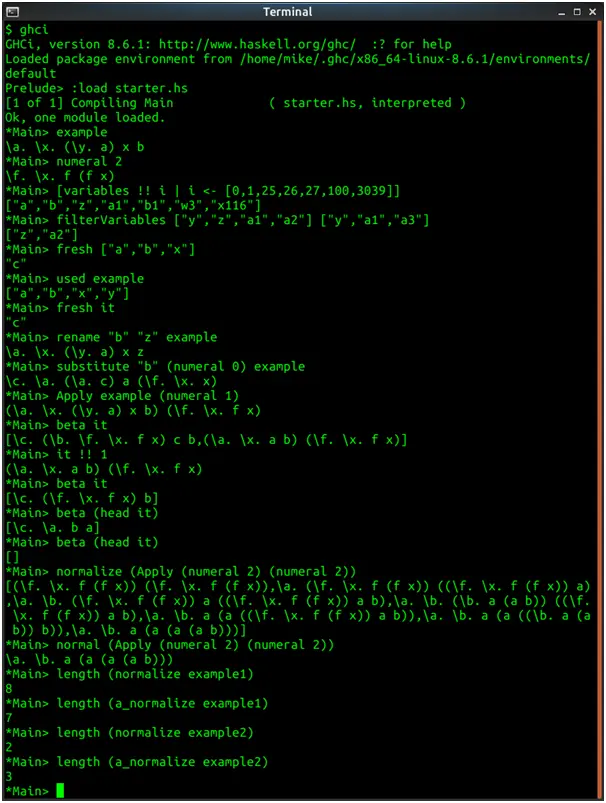
Screenshots of output

Source Code

type Var = String data Term = Variable Var | Lambda Var Term | Apply Term Term -- deriving Show instance Show Term where show = pretty example :: Term example = Lambda "a" (Lambda "x" (Apply (Apply (Lambda "y" (Variable "a")) (Variable "x")) (Variable "b"))) pretty :: Term -> String pretty = f 0 where f i (Variable x) = x f i (Lambda x m) = if i /= 0 then "(" ++ s ++ ")" else s where s = "\\" ++ x ++ ". " ++ f 0 m f i (Apply n m) = if i == 2 then "(" ++ s ++ ")" else s where s = f 1 n ++ " " ++ f 2 m ------------------------- Assignment 1 numeral :: Int -> Term numeral i = Lambda "f" (Lambda "x" (ni i "x" "f")) where ni 0 x _ = Variable x ni n x f = Apply (Variable f) (ni (n - 1) x f) ------------------------- merge :: Ord a => [a] -> [a] -> [a] merge xs [] = xs merge [] ys = ys merge (x:xs) (y:ys) | x == y = x : merge xs ys | x <= y = x : merge xs (y:ys) | otherwise = y : merge (x:xs) ys ------------------------- Assignment 2 variables :: [Var] variables = [[c] | c <- ['a'..'z']] ++ [[c]++(show i) |i <- [1..], c <- ['a'..'z']] filterVariables :: [Var] -> [Var] -> [Var] filterVariables xs ys = filter (\x -> not (elem x ys)) xs fresh :: [Var] -> Var fresh xs = head (filterVariables variables xs) used :: Term -> [Var] used (Variable v) = [v] used (Lambda v t) = merge [v] (used t) used (Apply x y) = merge (used x) (used y) ------------------------- Assignment 3 rename :: Var -> Var -> Term -> Term rename x y (Variable z) = Variable (if z == x then y else z) rename x y l@(Lambda z n) = if z == x then l else Lambda z (rename x y n) rename x y (Apply n m) = Apply (rename x y n) (rename x y m) substitute :: Var -> Term -> Term -> Term substitute x n (Variable y) = if y == x then n else Variable y substitute x n l@(Lambda y m) = if y == x then l else Lambda z (substitute x n ((rename y z) m)) where z = fresh ((used m) ++ (used n) ++ [x]) substitute x n (Apply m1 m2) = Apply (substitute x n m1) (substitute x n m2) ------------------------- Assignment 4 beta :: Term -> [Term] beta (Apply l@(Lambda x n) m) = [substitute x m n] ++ (map (\x -> (Apply x m)) (beta l)) ++ (map (\y -> (Apply l y)) (beta m)) beta (Variable _) = [] beta (Lambda x n1) = map (\y-> Lambda x y) (beta n1) beta (Apply n m) = (map (\x -> (Apply x m)) (beta n)) ++ (map (\y -> (Apply n y)) (beta m)) normalize :: Term -> [Term] normalize t = t : (eval_beta t) where eval_beta a = case beta a of [] -> [] (x:xs) -> x : (eval_beta x) normal :: Term -> Term normal t = last (normalize t) ------------------------- a_beta :: Term -> [Term] a_beta (Apply l@(Lambda x n) m) = (map (\x -> (Apply x m)) (a_beta l)) ++ (map (\y -> (Apply l y)) (a_beta m)) ++ [substitute x m n] a_beta (Variable _) = [] a_beta (Lambda x n1) = map (\y-> Lambda x y) (a_beta n1) a_beta (Apply n m) = (map (\x -> (Apply x m)) (a_beta n)) ++ (map (\y -> (Apply n y)) (a_beta m)) a_normalize :: Term -> [Term] a_normalize t = t : (eval_beta t) where eval_beta a = case a_beta a of [] -> [] (x:xs) -> x : (eval_beta x) a_normal :: Term -> Term a_normal t = last (a_normalize t) ------------------------- example1 :: Term example1 = Apply (Apply (numeral 2) (numeral 2)) (Variable "s") example2 :: Term example2 = Apply (Lambda "p" (Lambda "q" (Variable "q"))) (Apply (Lambda "a" (Variable "b")) (Lambda "c" (Variable "d")))