Create A Program To Manipulate Binary Trees In Haskell Language Assignment Solution

Instructions

Objective

Write a haskell assignment program to Manipulate binary trees.

Requirements and Specifications

Given a binary search tree t, bstInsert x t is a binary search tree formed by

-- replacing a Tip in t with (Bin x Tip Tip) or t, if t already contains x.

--

-- *HW2> bstInsert 3 bst1

-- Bin 2 (Bin 0 Tip Tip) (Bin 4 (Bin 3 Tip Tip) Tip)

-- *HW2> bstInsert 1 bst1

-- Bin 2 (Bin 0 Tip (Bin 1 Tip Tip)) (Bin 4 Tip Tip)

-- *HW2> bstInsert (-1) bst1

-- Bin 2 (Bin 0 (Bin (-1) Tip Tip) Tip) (Bin 4 Tip Tip)

-- *HW2> bstInsert 2 bst1

-- Bin 2 (Bin 0 Tip Tip) (Bin 4 Tip Tip)

--

-- Note: bstInsert should assume that the tree is a valid binary search tree, meaning

-- that the root is greater than all elements in its left subtree and less than all

-- elements in its right subtree. If bstInsert is given a binary search tree, its output

-- must also be a binary search tree. If bstInsert is given a tree that is not a binary

-- search tree, any convenient output is acceptable.

bstInsert :: Ord a => a -> Tree a -> Tree a

bstInsert = undefined

Screenshots of output

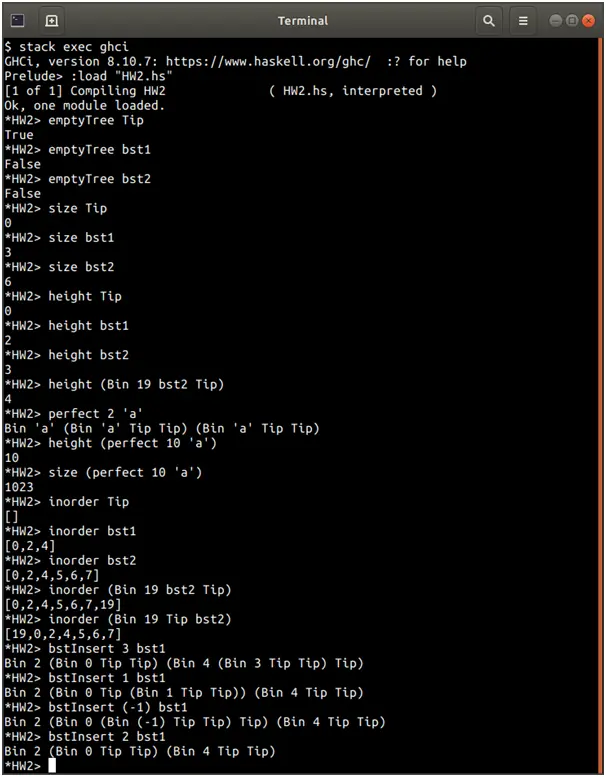
Source Code

module HW2 where data List a = Nil | Cons a (List a) deriving (Show, Eq, Ord) data Tree a = Tip | Bin a (Tree a) (Tree a) deriving (Show, Eq, Ord) bst1 = Bin 2 (Bin 0 Tip Tip) (Bin 4 Tip Tip) bst2 = Bin 5 bst1 (Bin 7 (Bin 6 Tip Tip) Tip) -- 0. emptyTree t returns True if and only if its argument is Tip emptyTree :: Tree a -> Bool emptyTree Tip = True emptyTree _ = False -- As with HW1, replace each incorrect definition with a correct definition. For example, -- -- emptyTree Tip = True -- emptyTree _ = False -- 1. size t returns the total number of elements in t. This is the same as the number of -- Bin nodes in t. -- -- *HW2> size bst1 -- 3 -- *HW2> size bst2 -- 6 size :: Tree a -> Int size Tip = 0 size (Bin _ lt rt) = size lt + size rt + 1 -- 2. height t returns the height of t. This is the length of the longest path from the -- root node to a Tip. -- -- *HW2> height Tip -- 0 -- *HW2> height bst1 -- 2 -- *HW2> height bst2 -- 3 -- *HW2> height (Bin 19 bst2 Tip) -- 4 height :: Tree a -> Int height Tip = 0 height (Bin _ lt rt) = max (height lt) (height rt) + 1 -- 3. perfect n a returns a "perfect" binary tree of height n containing the value -- a for all nodes. In a perfect binary tree, all nodes have either two children -- or no children. -- -- *HW2> perfect 2 'a' -- Bin 'a' (Bin 'a' Tip Tip) (Bin 'a' Tip Tip) -- -- In general, we expect the following rules to hold: -- for all positive integers n and all arbitrary values x: -- height (perfect n x) == n -- size (perfect n x) == 2^n - 1 perfect :: Int -> a -> Tree a perfect 0 _ = Tip perfect 1 x = Bin x Tip Tip perfect n x = Bin x (perfect (n - 1) x) (perfect (n - 1) x) -- 4. inorder t returns a list containing all the elements of t in order, meaning the -- elements of the left subtree (in order), followed by the root, followed by the -- elements of the right subtree (in order). -- -- *HW2> inorder Tip -- [] -- *HW2> inorder bst1 -- [0,2,4] -- *HW2> inorder bst2 -- [0,2,4,5,6,7] -- *HW2> inorder (Bin 19 bst2 Tip) -- [0,2,4,5,6,7,19] -- *HW2> inorder (Bin 19 Tip bst2) -- [19,0,2,4,5,6,7] -- -- In general, for all binary trees t, we expect -- length (inorder t) == size t -- -- Note: the order in "inorder" is the order of items in the tree, not their sorted -- order. Your implementation should not perform any comparisons. inorder :: Tree a -> [a] inorder Tip = [] -- if tree, get inorder list from left, append to root element and then append -- to right inorder list inorder (Bin x lt rt) = inorder lt ++ [x] ++ inorder rt -- 5. Given a binary search tree t, bstInsert x t is a binary search tree formed by -- replacing a Tip in t with (Bin x Tip Tip) or t, if t already contains x. -- -- *HW2> bstInsert 3 bst1 -- Bin 2 (Bin 0 Tip Tip) (Bin 4 (Bin 3 Tip Tip) Tip) -- *HW2> bstInsert 1 bst1 -- Bin 2 (Bin 0 Tip (Bin 1 Tip Tip)) (Bin 4 Tip Tip) -- *HW2> bstInsert (-1) bst1 -- Bin 2 (Bin 0 (Bin (-1) Tip Tip) Tip) (Bin 4 Tip Tip) -- *HW2> bstInsert 2 bst1 -- Bin 2 (Bin 0 Tip Tip) (Bin 4 Tip Tip) -- -- Note: bstInsert should assume that the tree is a valid binary search tree, meaning -- that the root is greater than all elements in its left subtree and less than all -- elements in its right subtree. If bstInsert is given a binary search tree, its output -- must also be a binary search tree. If bstInsert is given a tree that is not a binary -- search tree, any convenient output is acceptable. bstInsert :: Ord a => a -> Tree a -> Tree a bstInsert x Tip = Bin x Tip Tip bstInsert x (Bin y lt rt) = -- if equal to the value, return the tree if x == y then (Bin x lt rt) -- if smaller than value in root, recurse to insert at left subtree else if x < y then Bin y (bstInsert x lt) rt -- else, it's greated than value in root, recurse to insert at right subtree else Bin y lt (bstInsert x rt)