Program To Compute Matrix Computations in Python Assignment Solution

Instructions

Objective

Write a python assignment to compute matrix computations.

Requirements and Specifications

Source Code

import numpy as np import warnings def swapRows(A, i, j): """ interchange two rows of A operates on A in place """ tmp = A[i].copy() A[i] = A[j] A[j] = tmp def relError(a, b): """ compute the relative error of a and b """ with warnings.catch_warnings(): warnings.simplefilter("error") try: return np.abs(a-b)/np.max(np.abs(np.array([a, b]))) except: return 0.0 def rowReduce(A, i, j, pivot): """ reduce row j using row i with pivot pivot, in matrix A operates on A in place """ factor = A[j][pivot] / A[i][pivot] for k in range(len(A[j])): # we allow an accumulation of error 100 times larger than a single computation # this is crude but works for computations without a large dynamic range if relError(A[j][k], factor * A[i][k]) < 100 * np.finfo('float').resolution: A[j][k] = 0.0 else: A[j][k] = A[j][k] - factor * A[i][k] # stage 1 (forward elimination) def forwardElimination(B): """ Return the row echelon form of B """ A = B.copy().astype(float) m, n = np.shape(A) for i in range(m-1): # Let lefmostNonZeroCol be the position of the leftmost nonzero value # in row i or any row below it leftmostNonZeroRow = m leftmostNonZeroCol = n ## for each row below row i (including row i) for h in range(i,m): ## search, starting from the left, for the first nonzero for k in range(i,n): if (A[h][k] != 0.0) and (k < leftmostNonZeroCol): leftmostNonZeroRow = h leftmostNonZeroCol = k break # if there is no such position, stop if leftmostNonZeroRow == m: break # If the leftmostNonZeroCol in row i is zero, swap this row # with a row below it # to make that position nonzero. This creates a pivot in that position. if (leftmostNonZeroRow > i): swapRows(A, leftmostNonZeroRow, i) # Use row reduction operations to create zeros in all positions # below the pivot. for h in range(i+1,m): rowReduce(A, i, h, leftmostNonZeroCol) return A #################### # If any operation creates a row that is all zeros except the last element, # the system is inconsistent; stop. def inconsistentSystem(A): """ B is assumed to be in echelon form; return True if it represents an inconsistent system, and False otherwise """ m, n = np.shape(A) for i in range(m): for j in range(n): if (A[i][j] != 0): if (j == n-1): return True else: break return False def backsubstitution(B): """ return the reduced row echelon form matrix of B """ A = B.copy().astype(float) m, n = np.shape(A) for i in range(m): # If row i is all zeros, or if i exceeds the number of rows in A, stop. for j in range(n): if A[i][j] != 0.0: break if j == n-1: return A pivot = j # If row i has a nonzero pivot value, divide row i by its pivot value. # This creates a 1 in the pivot position. 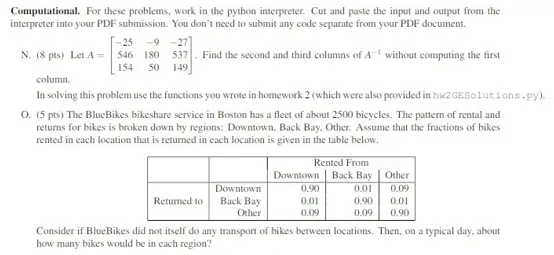A[i] = A[i] / A[i][pivot] for j in range(i+1, m): rowReduce(A, i, j, pivot) return A ##################### print("N (8 pts)") B = backsubstitution(np.array([[-25, -29, -27, 1, 0, 0], [546, 180, 537, 0, 1, 0], [154, 50, 149, 0, 0, 1]])) swapRows(B, 0, 2) B = backsubstitution(B) swapRows(B, 0, 2) A2 = B[0:3, 4] A3 = B[0:3, 5] print("Second column of inversed matrix:", A2) print("Third column of inversed matrix:", A3) print("\n\n") print("O (5 pts)") print("Let A is a matrix of rearrangement, mentioned in the assignment") A = [[0.9, 0.01, 0.09], [0.01, 0.9, 0.01], [0.09, 0.09, 0.9]] print("A =",A) print("Let vector X represents initial distribution of bike fleet among 3 locations (i.e. [1000, 1000, 500])") print("Then A*X gives us distribution after first dat, A^2*X gives distribution after 2 days.... A^k*2 - distribution after k days") print("Let's calculate A^100") deg = np.eye(3) for _ in range(100): deg = np.matmul(deg, A) print("A^100 =") print(deg) print("We see that each row contains approximately equal numbers. It is the property of stochastic matrix (A is stochastic):") print("A^k converges to matrix with constant value in each row") print("When we calculate product R = A^100*X, we obtain the following matrix R (for any valid initial vector X):") fleet = 2500 R = [deg[0][0] * 2500, deg[1][0] * 2500, deg[2][0] * 2500] print("R =", R) print("So, the expected number of bikes in downtown is approx", int(R[0]), ", expected number of bikes in Back Bay is approx", int(R[1]), "expected number of bikes in Other locations is approx", int(R[2])) Contact Details Address: 5209 Cedar Glenn