Python Program to Implement Model Fitting Assignment Solution

Instructions

Objective

Write a python program to implement model fitting.

Requirements and Specifications

Source Code

!pip install otter-grader # Initialize Otter import otter grader = otter.Notebook("lab8.ipynb") # Lab 8: Fitting Models to Data In this lab, you will practice using a numerical optimization package `cvxpy` to compute solutions to optimization problems. The example we will use is a linear fit and a quadratic fit. import pandas as pd import numpy as np %matplotlib inline import matplotlib.pyplot as plt import seaborn as sns ## Objectives for Lab 8: Models and fitting models to data is a common task in data science. In this lab, you will practice fitting models to data. The models you will fit are: * Linear fit * Normal distribution ## Boston Housing Dataset from sklearn.datasets import load_boston boston_dataset = load_boston() print(boston_dataset['DESCR']) housing = pd.DataFrame(boston_dataset['data'], columns=boston_dataset['feature_names']) housing['MEDV'] = boston_dataset['target'] housing.head() fig, ax = plt.subplots(figsize=(10, 7)) sns.scatterplot(x='LSTAT', y='MEDV', data=housing) plt.show() 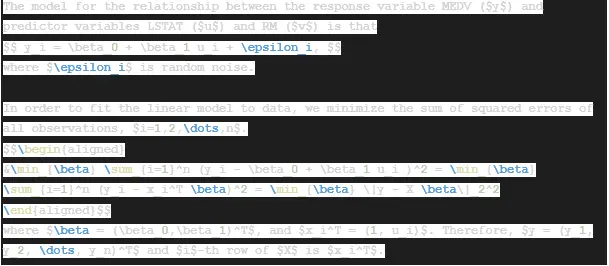The model for the relationship between the response variable MEDV ($y$) and predictor variables LSTAT ($u$) and RM ($v$) is that $$ y_i = \beta_0 + \beta_1 u_i + \epsilon_i, $$ where $\epsilon_i$ is random noise. In order to fit the linear model to data, we minimize the sum of squared errors of all observations, $i=1,2,\dots,n$. $$\begin{aligned} &\min_{\beta} \sum_{i=1}^n (y_i - \beta_0 + \beta_1 u_i )^2 = \min_{\beta} \sum_{i=1}^n (y_i - x_i^T \beta)^2 = \min_{\beta} \|y - X \beta\|_2^2 \end{aligned}$$ where $\beta = (\beta_0,\beta_1)^T$, and $x_i^T = (1, u_i)$. Therefore, $y = (y_1, y_2, \dots, y_n)^T$ and $i$-th row of $X$ is $x_i^T$. ## Question 1: Constructing Data Variables Define $y$ and $X$ from `housing` data. y = housing['MEDV'] X1 = housing['LSTAT'].to_frame() X1.insert(0, 'intercept', np.ones((len(y),1))) #X.insert(0, 'intercept', X1) grader.check("q1") ## Installing CVXPY First, install `cvxpy` package by running the following bash command: !pip install cvxpy ## Question 2: Fitting Linear Model to Data Read this example of how cvxpy problem is setup and solved: https://www.cvxpy.org/examples/basic/least_squares.html The usage of cvxpy parallels our conceptual understanding of components in an optimization problem: * `beta` are the variables $\beta$ * `loss` is sum of squared errors * `prob` minimizes the loss by choosing $\beta$ Make sure to extract the data array of data frames (or series) by using `values`: e.g., `X.values` beta2 import cvxpy as cp beta2 = cp.Variable(2) loss2 = cp.sum_squares(y.values-X1.values @ beta2) prob2 = cp.Problem(cp.Minimize(loss2)) prob2.solve() yhat2 = X1.values@beta2.value grader.check("q2") ## Question 3: Visualizing resulting Linear Fit Visualize fitted model by plotting `LSTAT` by `MEDV`. fig, ax = plt.subplots(figsize=(10, 7)) sns.scatterplot(x='LSTAT', y='MEDV', data=housing, ax = ax, label='Data') sns.scatterplot(housing['LSTAT'], yhat2, label='Fit', ax = ax) plt.legend() plt.show() ## Question 4: Fitting Quadratic Model to Data Add a column of squared `LSTAT` values to `X`. The new model is, Then, fit a quadratic model to data. X2 = X1.copy() X2.insert(2, 'LSTAT^2', X2['LSTAT']**2) beta4 = cp.Variable(3) loss4 = cp.sum_squares(y.values-X2.values @ beta4) prob4 = cp.Problem(cp.Minimize(loss4)) prob4.solve() yhat4 = X2.values@beta4.value grader.check("q4a") Visualize quadratic fit: fig, ax = plt.subplots(figsize=(10, 7)) sns.scatterplot(x='LSTAT', y='MEDV', data=housing, ax = ax, label='Data') sns.scatterplot(housing['LSTAT'], yhat4, label='Fit', ax = ax) plt.legend() plt.show() --- To double-check your work, the cell below will rerun all of the autograder tests. grader.check_all() ## Submission Make sure you have run all cells in your notebook in order before running the cell below, so that all images/graphs appear in the output. The cell below will generate a zip file for you to submit. **Please save before exporting!** # Save your notebook first, then run this cell to export your submission. grader.export()